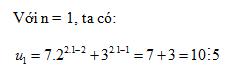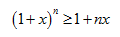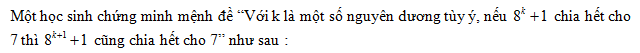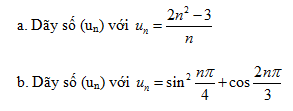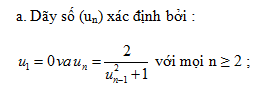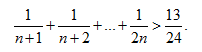
Giải câu 1 trang 100 SGK Đại số và Giải tích 11 Nâng cao

Bài trước
Bài sau  

Chứng minh rằng

Bài 1. Chứng minh rằng với mọi số nguyên dương n, ta luôn có đẳng thức sau :

\(1 + 2 + 3 + ... + n = {{n\left( {n + 1} \right)} \over 2}\)   (1)

Giải:

+) Với n = 1 ta có \(1 = {{1\left( {1 + 1} \right)} \over 2}\) (đúng).

Vậy (1) đúng với n = 1

+) Giả sử (1) đúng với \(n = k\), tức là ta có:

\(1 + 2 + 3 + ... + k = {{k\left( {k + 1} \right)} \over 2}\)

Ta chứng minh (1) đúng với \(n = k + 1\) tức là phải chứng minh :

\(1 + 2 + ... + k + \left( {k + 1} \right) = {{\left( {k + 1} \right)\left( {k + 2} \right)} \over 2}\)

Thật vậy ta có :

\(\eqalign{
& 1 + 2 + ... + k + \left( {k + 1} \right) \cr
& = {{k\left( {k + 1} \right)} \over 2} + \left( {k + 1} \right) \cr
& = {{k\left( {k + 1} \right) + 2\left( {k + 1} \right)} \over 2} \cr
& = {{\left( {k + 1} \right)\left( {k + 2} \right)} \over 2} \cr} \)

Vậy (1) đúng với \(n = k + 1\) do đó (1) đúng với mọi n nguyên dương.

Bài trước
In bài này
Bài sau  
Các bài học liên quan
Các chương học và chủ đề lớn
Học tốt các môn khác lớp 11

Bài học nổi bật nhất

Đề thi lớp 11 mới cập nhật