Giải câu 37 trang 68 SGK Hình học 11 Nâng cao
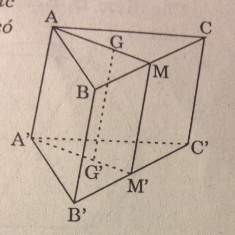
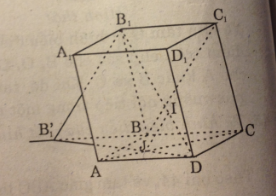
Cho hình hộp ABCD.A’B’C’D’. Chứng minh rẳng a. mp(BDA’) // mp(B’D’C) b.Đường chéo AC’ đi qua các trọng tâm G1, G2 của hai tam giác BDA’ và B’D’C
- Bài học cùng chủ đề:
- Câu 38 trang 68 SGK Hình học 11 Nâng cao
- Câu 39 trang 68 SGK Hình học 11 Nâng cao
- Ngữ pháp tiếng anh hay nhất
Cho hình hộp ABCD.A’B’C’D’. Chứng minh rẳng
a. mp(BDA’) // mp(B’D’C)
b.Đường chéo AC’ đi qua các trọng tâm G1, G2 của hai tam giác BDA’ và B’D’C
c. G1 và G2 chia đoạn AC’ thành ba phần bằng nhau
d. Các trung điểm của sáu cạnh BC, CD, DD’, D’A’, A’B’,B’B cùng nằm trên một mặt phẳng
Giải:
a) Chứng minh ( BDA’) // (B’D’C)
Ta có tứ giác BB’D’D và A’B’CD là các hình bình hành nên : BD // B’D’ và DA’ // B’C
⇒ hai mặt phẳng (BDA’) và (B’D’C) có các cặp đường thẳng cắt nhau và song song nhau từng đôi một nên chúng song song.
Vậy (BDA’) // (B’D’C).
b) Chứng minh G1 , G2 ∈ AC’

Gọi O, O’ lần lượt là tâm của hình bình hành ABCD và A’B’C’D’.
Trong mặt phẳng (AA’C’C) gọi G1 , G2 lần lượt là giao điểm của AC’ với A’O và O’C. Ta chứng minh G1, G2 lần lượt là trong tâm của ∆A’BD và ∆CB’D’.
Thật vậy, ta có ∆G1OA đồng dạng ∆G1A’C’ ( vì AC // A’C’)
\( \Rightarrow {{{G_1}O} \over {{G_1}A'}} = {{OA} \over {A'C'}} = {1 \over 2} \Rightarrow {{A'{G_1}} \over {A'O}} = {2 \over 3}\)
⇒ G1 là trọng tâm ∆A’BD.
Tương tự, G2 là trọng tâm ∆CB’D’. Vậy AC’ đi qua G1, G2 .
c) Chứng minh AG1 = G1G2 = G2C’
Theo câu trên , ta có:
\({{A{G_1}} \over {{G_1}C'}} = {{AO} \over {A'C'}} = {1 \over 2}\) ( vì ∆G1OA đồng dạng ∆G1A’C’) \( \Rightarrow A{G_1} = {1 \over 3}AC'\) (1)
Tương tự: \({{C'{G_2}} \over {{G_2}A}} = {{C'O'} \over {CA}} = {1 \over 2}\) ( vì ∆G2C’O' đồng dạng ∆G2AC) \( \Rightarrow C'{G_2} = {1 \over 3}AC'\) (2)
Từ (1) và (2) suy ra: AG1 = G1G2 = G2C’.
d)

Gọi M, N, P, Q, S, R lần lượt là trung điểm của các cạnh AB, AD, DD’, C’D’, C’B’, B’B.
Ta có: \(\left\{ {\matrix{ {MN//BD} \cr {SP//BD} \cr } } \right. \Rightarrow MN//SP\)
Gọi (α) = (MN, SP)
Ta có : \(\left\{ {\matrix{ {PQ//DC'} \cr {MS//AB'} \cr } } \right. \Rightarrow PQ//MS\)
( vì DC’ // AB’)
⇒ PQ ⊂ (α) do đó Q ∈ (α).
Tương tự: QR // MN ⇒ QR ⊂ (α) do đó R ∈ (α).
Vậy M, N, P, Q, R, S ∈ (α).
Mặt khác vì \(\left\{ {\matrix{ {MS//AB'} \cr {NP//AD'} \cr } } \right.\) nên (MNPQRS) // (AB’D').
- Chương i. hàm số lượng giác và phương trình lượng giác
- Chương ii. tổ hợp và xác suất
- Chương iii. dãy số. cấp số cộng và cấp số nhân
- Chương iv. giới hạn
- Chương v. đạo hàm
- Ôn tập cuối năm đại số và giải tích
- Chương i. phép dời hình và đồng dạng trong mặt phẳng
- Chương ii: đường thẳng và mặt phẳng trong không gian. quan hệ song song
- Chương iii: vectơ trong không gian. quan hệ vuông góc
- Ôn tập cuối năm hình học