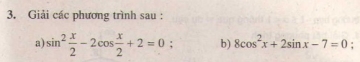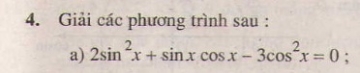Giải bài 3 trang 28 sgk giải tích 11
Chia sẻ trang này
Bài 3. Giải các phương trình sau:
- Bài học cùng chủ đề:
- Bài 4 trang 29 sgk giải tích 11
- Bài 5 trang 29 sgk giải tích 11
- Bài 6 trang 29 sgk giải tích 11
- Ngữ pháp tiếng anh hay nhất
Bài 3. Giải các phương trình sau:
a) \( cos (x - 1) =\frac{2}{3}\)
b) \(cos 3x = cos 12^0\)
c) \(cos (\frac{3x}{2}-\frac{\pi}{4})=-\frac{1}{2}\)
d) \(cos^22x =\frac{1}{4}\)
Trả lời:
a)
\(cos (x - 1) = \frac{2}{3} \Leftrightarrow \Bigg \lbrack\begin{matrix} x - 1 = arccos \frac{2}{3} + k2\pi\\ \\ x - 1 = - arccos \frac{2}{3} + k2\pi \end{matrix}\)
\(\Leftrightarrow \Bigg \lbrack\begin{matrix} x = 1 + arccos \frac{2}{3} + k2\pi , (k \in Z) \\ \\ x = 1 - arccos \frac{2}{3} + k2\pi , (k \in Z). \end{matrix}\)
Vậy nghiệm phương trình là \(x = 1 + arccos \frac{2}{3} + k2\pi , (k \in Z)\) hoặc \(x = 1 - arccos \frac{2}{3} + k2\pi , (k \in Z).\)
b)
\(cos 3x = cos 12^0\Leftrightarrow 3x = \pm 12^0 + k360^0 (k\in \mathbb{Z})\)
\(\Leftrightarrow x = \pm 4^0 + k120^0 , (k \in Z).\)
Vậy nghiệm phương trình là \(x = \pm 4^0 + k120^0 , (k \in Z).\)
c)
\(cos\left ( \frac{3x}{2}-\frac{\pi }{4} \right )=-\frac{1}{2}\)
\(\Leftrightarrow cos\left ( \frac{3x}{2}-\frac{\pi }{4} \right )=cos\left ( \pi -\frac{\pi }{3} \right )\)
\(\Leftrightarrow \Bigg \lbrack\begin{matrix} \frac{3x}{2}-\frac{\pi }{4}=\frac{2\pi }{3}+k2 \pi\\ \\ \frac{3x}{2}-\frac{\pi }{4}=-\frac{2\pi }{3}+k2 \pi \end{matrix},(k\in \mathbb{Z})\)
\(\Leftrightarrow \Bigg \lbrack\begin{matrix} x=\frac{11\pi }{18}+k.\frac{4\pi }{3} \\ \\ x=-\frac{5\pi}{18}+k.\frac{4\pi }{3} \end{matrix},(k\in \mathbb{Z})\)
Vậy nghiệm phương trình là \(x=\frac{11\pi }{18}+\frac{4 k\pi }{3}\) và \(x=-\frac{5\pi}{18}+\frac{4 k\pi }{3} (k\in \mathbb{Z})\)
d)
\(cos^22x =\frac{1}{4}\Leftrightarrow\)
\(\Bigg \lbrack\begin{matrix} cos2x=\frac{1}{2}\\ \\ cos2x=-\frac{1}{2} \end{matrix}\Leftrightarrow \Bigg \lbrack\begin{matrix} cos2x=cos \frac{\pi }{3}\\ \\ cos2x= cos\frac{2\pi }{3} \end{matrix}\)
\(\Leftrightarrow \Bigg \lbrack\begin{matrix} 2x=\pm \frac{\pi }{3} + k2 \pi\\ \\ 2x=\pm \frac{2\pi }{3} + k2 \pi \end{matrix}, k\in \mathbb{Z}\)
\(\Leftrightarrow \Bigg \lbrack\begin{matrix} x= \pm \frac{\pi }{6} +k \pi\\ \\ x= \pm \frac{\pi }{3} +k \pi \end{matrix}, k\in \mathbb{Z}\)
Vậy nghiệm phương trình là \(x= \pm \frac{\pi }{6} +k \pi\) và \(x= \pm \frac{\pi }{3} +k \pi, k\in \mathbb{Z}\).
dayhoctot.com
Chia sẻ trang này
Các bài học liên quan
Các chương học và chủ đề lớn
