Giải câu 4 trang 78 SGK Hình học 11 Nâng cao
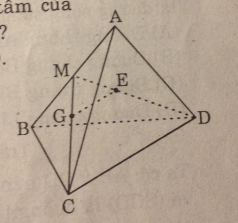
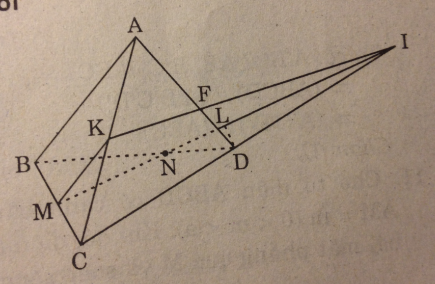
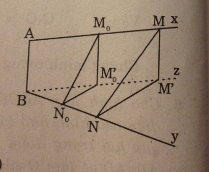
Cho hai hình bình hành ABCD VÀ ABEF nằm trong hai mặt phẳng khác nhau. Lấy các điểm M, N lần lượt thuộc các đường chéo AC, BF sao cho MC = 2AM, NF = 2BN. Qua M, N, kẻ các đường thẳng song song với AB cắt các cạnh AD, AF lần lượt tại M1, N1. Chứng minh rằng:
- Bài học cùng chủ đề:
- Câu 5 trang 78 SGK Hình học 11 Nâng cao
- Câu 6 trang 78 SGK Hình học 11 Nâng cao
- Câu 7 trang 78 SGK Hình học 11 Nâng cao
- Ngữ pháp tiếng anh hay nhất
Cho hai hình bình hành ABCD VÀ ABEF nằm trong hai mặt phẳng khác nhau. Lấy các điểm M, N lần lượt thuộc các đường chéo AC, BF sao cho MC = 2AM, NF = 2BN. Qua M, N, kẻ các đường thẳng song song với AB cắt các cạnh AD, AF lần lượt tại M1, N1. Chứng minh rằng:
a. MN // DE
b. M1N1 // mp(DEF)
c. mp(MNN1M1) // mp(DEF)
Giải:

a. Gọi O là tâm hình bình hành ABCD, ta có AO là trung tuyến và \({{AM} \over {AO}} = {{2AM} \over {AC}} = {2 \over 3}\)
⇒ M là trọng tâm của tam giác ABD , tương tự N là trọng tâm tam giác ABE
Gọi I là trung điểm của AB thì M, N lần lượt trên DI và EI
Trong tam giác IDE ta có: \({{IM} \over {ID}} = {{IN} \over {IE}} = {1 \over 3}\) nên MN // DE và \(MN = {1 \over 3}DE\)
b. Trong ∆FAB: NN1 // AB ⇒ \({{A{N_1}} \over {AF}} = {{BN} \over {BF}} = {1 \over 3}\)
Trong ∆DAB: MM1 // AB ⇒ \({{A{M_1}} \over {AD}} = {{DM} \over {DI}} = {1 \over 3}\)
Do đó \({{A{N_1}} \over {AF}} = {{A{M_1}} \over {AD}}\) nên M1N1 // DF
Mà DF ⊂ (DEF) suy ra M1N1 // mp(DEF)
c. Ta có : M1N1 // DF , NN1 // EF
mà M1N1 và NN1 cắt nhau và nằm trong mp(MNN1M1), còn DF và EF cắt nhau và nằm trong mp(DEF)
Vậy mp(MNN1M1) // mp(DEF)
- Chương i. hàm số lượng giác và phương trình lượng giác
- Chương ii. tổ hợp và xác suất
- Chương iii. dãy số. cấp số cộng và cấp số nhân
- Chương iv. giới hạn
- Chương v. đạo hàm
- Ôn tập cuối năm đại số và giải tích
- Chương i. phép dời hình và đồng dạng trong mặt phẳng
- Chương ii: đường thẳng và mặt phẳng trong không gian. quan hệ song song
- Chương iii: vectơ trong không gian. quan hệ vuông góc
- Ôn tập cuối năm hình học