Giải câu 20 trang 103 SGK Hình học 11 Nâng cao

• Ngữ pháp tiếng anh hay nhất

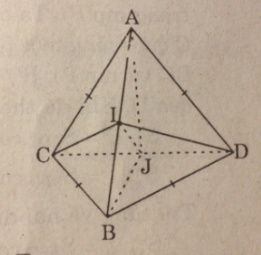
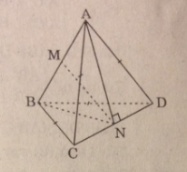
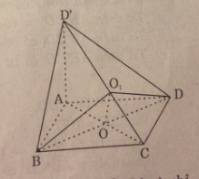
a. Cho tứ diện ABCD có AB ⊥ CD, AC ⊥ BD. Chứng minh rằng AD ⊥ BC. Vậy, các cạnh đối diện của tứ diện đó vuông góc với nhau. Tứ diện như thế gọi là tứ diện trực tâm.

b. Chứng minh các mệnh đề sau đây là tương đương :

i. ABCD là tứ diện trực tâm.

ii. Chân đường cao của tứ diện hạ từ một đỉnh trùng với trực tâm của mặt đối diện.

iii. \(A{B^2} + C{D^2} = A{C^2} + B{D^2} = A{D^2} + B{C^2}\)

c. Chứng minh rằng bốn đường cao của tứ diện trực tâm đồng quy tại một điểm. Điểm đó gọi là trực tâm của tứ diện nói trên.

Giải

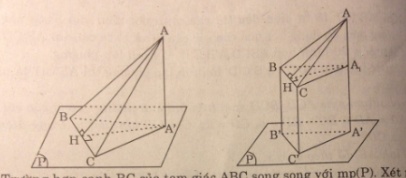
a. Kẻ AH ⊥ (BCD), H ϵ (BCD)

Ta có \(\left\{ {\matrix{   {CD \bot AH}  \cr   {CD \bot AB}  \cr } } \right. \Rightarrow CD \bot \left( {ABH} \right)\)

Mà BH ⊂ (ABH) nên CD ⊥ BH (1)

Tương tự \(\left\{ {\matrix{   {BD \bot AH}  \cr   {BD \bot AC}  \cr } } \right. \Rightarrow BD \bot \left( {ACH} \right) \Rightarrow BD \bot CH\,\left( 2 \right)\)

Từ (1) và (2) suy ra H là trực tâm tam giác BCD.

Ta có: \(\left\{ {\matrix{   {BC \bot AH}  \cr   {BC \bot DH}  \cr  } } \right. \Rightarrow BC \bot \left( {ADH} \right) \Rightarrow BC \bot AD.\)

b. Theo chứng minh câu a ta có i ⇔ ii

Mặt khác ta có

\(\eqalign{  & A{B^2} + C{D^2} = A{C^2} + B{D^2}  \cr  &  \Leftrightarrow {\overrightarrow {AB} ^2} + {\overrightarrow {CD} ^2} = {\overrightarrow {AC} ^2} + {\overrightarrow {BD} ^2}  \cr  &  \Leftrightarrow {\overrightarrow {AB} ^2} + {\left( {\overrightarrow {AD}  - \overrightarrow {AC} } \right)^2} = {\overrightarrow {AC} ^2} + {\left( {\overrightarrow {AD}  - \overrightarrow {AB} } \right)^2}  \cr  &  \Leftrightarrow \overrightarrow {AD} .\overrightarrow {AC}  = \overrightarrow {AD} .\overrightarrow {AB}   \cr  &  \Leftrightarrow \overrightarrow {AD} .\left( {\overrightarrow {AC}  - \overrightarrow {AB} } \right) = 0  \cr  &  \Leftrightarrow \overrightarrow {AD} .\overrightarrow {BC}  = 0 \Leftrightarrow AD \bot BC \cr} \)

Tương tự AB ⊥ CD và AC ⊥ BD

Vậy i ⇔ iii

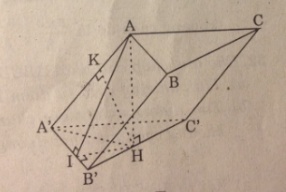
c. Gọi K là trực tâm tam giác ACD thì K nằm trên AI (với BI ⊥ CD). Từ đó suy ra AH và BK cắt nhau do chúng thuộc mp(ABI)

tương tự bốn đường cao của tứ diện trực tâm cắt nhau đôi một và không cùng nằm trên một mặt phẳng nên chúng đồng quy.

Trên đây là bài học "Giải câu 20 trang 103 SGK Hình học 11 Nâng cao" mà dayhoctot.com muốn gửi tới các em. Để rèn luyện về kỹ năng làm bài thi và kiểm tra các em tham khảo tại chuyên mục "Đề thi học kì 1 lớp 11" nhé.

Nếu thấy hay, hãy chia sẻ tới bạn bè để cùng học và tham khảo nhé! Và đừng quên xem đầy đủ các bài Giải bài tập Toán Lớp 11 của dayhoctot.com.

• Từ khóa:
• Lớp 11
• Toán Lớp 11 Nâng Cao
• Môn Toán
• Bài 3: Đường thẳng vuông góc với mặt phẳng
• Văn mẫu lớp 11