Giải câu 27 trang 112 SGK Hình học 11 Nâng cao

Chia sẻ trang này

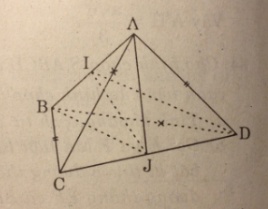
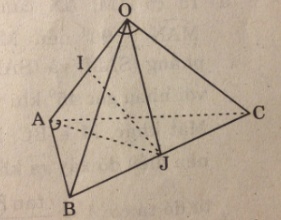
Cho hai tam giác ACD, BCD nằm trên hai mặt phẳng vuông góc với nhau và AC = AD = BC = BD = a, CD = 2x. Gọi I, J lần lượt là trung điểm của AB và CD.

a. Tính AB, IJ theo a và x.

b. Với giá trị nào của x thì hai mặt phẳng (ABC) và (ABD) vuông góc ?

Giải

a. Vì J là trung điểm của CD và AC = AD nên AJ ⊥ CD.

Do mp(ACD) ⊥ mp(BCD) nên AJ ⊥ mp(BCD)

Mặt khác, AC = AD = BC = BD nên tam giác AJB vuông cân, suy ra \(AB = AJ\sqrt 2 ,A{J^2} = {a^2} - {x^2}\,hay\,AJ = \sqrt {{a^2} - {x^2}} .\)

Vậy \(AB = \sqrt {2\left( {{a^2} - {x^2}} \right)} \) với a > x

Do IA = IB, tam giác AJB vuông tại J nên \(JI = {1 \over 2}AB,\) tức là \(IJ = {1 \over 2}\sqrt {2\left( {{a^2} - {x^2}} \right)} .\)

Rõ ràng là CI và DI vuông góc với AB.

Vậy mp(ABC) ⊥ mp(ABD) \( \Leftrightarrow \widehat {CID} = 90^\circ \)

\( \Leftrightarrow IJ = {1 \over 2}CD \Leftrightarrow {1 \over 2}\sqrt {2\left( {{a^2} - {x^2}} \right)} = {1 \over 2}.2x\)

\(\Leftrightarrow x = {{a\sqrt 3 } \over 3}\)

Trên đây là bài học "Giải câu 27 trang 112 SGK Hình học 11 Nâng cao" mà dayhoctot.com muốn gửi tới các em. Để rèn luyện về kỹ năng làm bài thi và kiểm tra các em tham khảo tại chuyên mục "Đề thi học kì 1 lớp 11" nhé.

Nếu thấy hay, hãy chia sẻ tới bạn bè để cùng học và tham khảo nhé! Và đừng quên xem đầy đủ các bài Giải bài tập Toán Lớp 11 của dayhoctot.com.