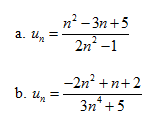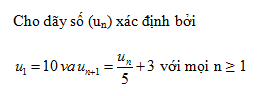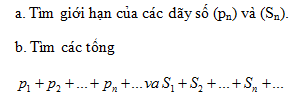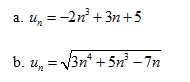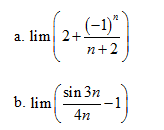
Giải câu 1 trang 130 SGK Đại số và Giải tích 11 Nâng cao

Bài trước
Bài sau  

Chứng minh rằng

Bài 1. Chứng minh rằng các dãy số với số hạng tổng quát sau đây có giới hạn 0 :

a.  \({{{{\left( { - 1} \right)}^n}} \over {n + 5}}\)

b.  \({{\sin n} \over {n + 5}}\)

c.  \({{\cos 2n} \over {\sqrt n + 1}}\)

Giải:

a. Ta có:

\(\left| {{{{{\left( { - 1} \right)}^n}} \over {n + 5}}} \right| = {1 \over {n + 5}} < {1 \over n}\,\text{ và }\,\lim {1 \over n} = 0 \Rightarrow \lim {{{{\left( { - 1} \right)}^n}} \over {n + 5}} = 0\)

b.  \(\left| {{{\sin n} \over {n + 5}}} \right| \le {1 \over {n + 5}} < {1 \over n}\,\text{ và }\,\lim {1 \over n} = 0 \Rightarrow \lim {{\sin n} \over {n + 5}} = 0\)

c.  \(\left| {{{\cos 2n} \over {\sqrt n + 1}}} \right| \le {1 \over {\sqrt n + 1}} < {1 \over {\sqrt n }},\lim{1 \over {\sqrt n }} = 0 \Rightarrow \lim {{\cos 2n} \over {\sqrt n + 1}} = 0\)

Bài trước
In bài này
Bài sau  
Các bài học liên quan
Các chương học và chủ đề lớn
Học tốt các môn khác lớp 11

Bài học nổi bật nhất

Đề thi lớp 11 mới cập nhật