Giải câu 3 trang 125 SGK Hình học 11 Nâng cao
Chia sẻ trang này
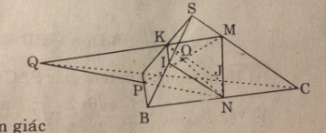
Cho tam giác ABC và hai hình vuông ABMN, ACPQ như hình 134.
- Bài học cùng chủ đề:
- Câu 4 trang 125 SGK Hình học 11 Nâng cao
- Câu 5 trang 125 SGK Hình học 11 Nâng cao
- Câu 6 trang 125 SGK Hình học 11 Nâng cao
- Ngữ pháp tiếng anh hay nhất
Cho tam giác ABC và hai hình vuông ABMN, ACPQ như hình 134.
a. Xác định phép quay biến tam giác ABQ thành tam giác ANC.
b. Chứng tỏ rằng hai đoạn thẳng BQ, CN bằng nhau và vuông góc với nhau.
c. Gọi O, O’ là tâm của các hình vuông, I là trung điểm của BC. Chứng minh rằng tam giác OIO’ là tam giác vuông cân.
Giải
a. Ta có: AB = AN, AQ = AC và góc (AB, AN) bằng góc (AQ, AC) = -90˚
Vậy phép quay tâm A, góc quay φ = -90˚ biến tam giác ABQ thành tam giác ANC.
b. Vì đoạn thẳng BQ biến thành đoạn thẳng NC nên BQ = NC và BQ ⊥ NC.
c. Theo kí hiệu hình bên thì OI // NC, \(OI = {1 \over 2}NC;O'I//QB,O'I = {1 \over 2}BQ\)
vậy từ câu b ta suy ra tam giác IOO’ vuông cân tại đỉnh I.
Chia sẻ trang này
Các bài học liên quan
Các chương học và chủ đề lớn
- Chương i. hàm số lượng giác và phương trình lượng giác
- Chương ii. tổ hợp và xác suất
- Chương iii. dãy số. cấp số cộng và cấp số nhân
- Chương iv. giới hạn
- Chương v. đạo hàm
- Ôn tập cuối năm đại số và giải tích
- Chương i. phép dời hình và đồng dạng trong mặt phẳng
- Chương ii: đường thẳng và mặt phẳng trong không gian. quan hệ song song
- Chương iii: vectơ trong không gian. quan hệ vuông góc
- Ôn tập cuối năm hình học
