Giải câu 2 trang 124 SGK Hình học 11 Nâng cao
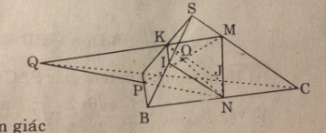
Cho tứ giác ABCD nội tiếp đường tròn (O). Gọi M, N, P, Q lần lượt là trung điểm các cạnh AB, BC, CD và DA. Kẻ MM’, NN’, PP’, QQ’ lần lượt vuông góc với CD, DA, AB, BC.
- Bài học cùng chủ đề:
- Câu 3 trang 125 SGK Hình học 11 Nâng cao
- Câu 4 trang 125 SGK Hình học 11 Nâng cao
- Câu 5 trang 125 SGK Hình học 11 Nâng cao
- Ngữ pháp tiếng anh hay nhất
Cho tứ giác ABCD nội tiếp đường tròn (O). Gọi M, N, P, Q lần lượt là trung điểm các cạnh AB, BC, CD và DA. Kẻ MM’, NN’, PP’, QQ’ lần lượt vuông góc với CD, DA, AB, BC.
a. Gọi I là giao điểm của MP và NQ. Phép đối xứng tâm ĐI biến các đường thẳng MM’, NN’, PP’, QQ’ thành những đường thẳng nào ?
b. Chứng tỏ rằng bốn đường thẳng MM’, NN’, PP’, QQ’ đồng quy tại một điểm. Nhận xét gì về vị trí điểm đồng quy và hai điểm I, O ?
Giải

a. MNPQ là hình bình hành nên I là trung điểm
của MP và NQ.
Phép đối xứng tâm ĐI biến điểm M thành điểm P, biến đường thẳng MM’ thành đường thẳng đi qua P và song song với MM’, tức là vuông góc với DC.
Vậy đường thẳng MM’ được biến thành đường thẳng PO. Hoàn toàn tương tự : đường thẳng NN’ biến thành đường QO, đường thẳng PP’ biến thành đường MO, đường thẳng QQ’ biến thành đường NO.
b. Vì bốn đường thẳng MO, NO, PO, QO đồng quy tại điểm O nên bốn đường thẳng MM’, NN’, PP’, QQ’ đồng quy tại O’ đối xứng với O qua điểm I.
- Chương i. hàm số lượng giác và phương trình lượng giác
- Chương ii. tổ hợp và xác suất
- Chương iii. dãy số. cấp số cộng và cấp số nhân
- Chương iv. giới hạn
- Chương v. đạo hàm
- Ôn tập cuối năm đại số và giải tích
- Chương i. phép dời hình và đồng dạng trong mặt phẳng
- Chương ii: đường thẳng và mặt phẳng trong không gian. quan hệ song song
- Chương iii: vectơ trong không gian. quan hệ vuông góc
- Ôn tập cuối năm hình học