Giải câu 25 trang 112 SGK Hình học 11 Nâng cao
Chia sẻ trang này
Cho hai mặt phẳng vuông góc (P) và (Q) có giao tuyến Δ. Lấy A, B cùng thuộc Δ và lấy C ϵ (P), D ϵ (Q) sao cho AC ⊥ AB, BD ⊥ AB và AB = AC = BD. Xác định thiết diện của tứ diện ABCD khi cắt bởi mặt phẳng (α) đi qua điểm A và vuông góc với CD. Tính diện tích thiết diện khi AC = AB = BD = a.
- Bài học cùng chủ đề:
- Câu 26 trang 112 SGK Hình học 11 Nâng cao
- Câu 27 trang 112 SGK Hình học 11 Nâng cao
- Câu 28 trang 112 SGK Hình học 11 Nâng cao
- Ngữ pháp tiếng anh hay nhất
Cho hai mặt phẳng vuông góc (P) và (Q) có giao tuyến Δ. Lấy A, B cùng thuộc Δ và lấy C ϵ (P), D ϵ (Q) sao cho AC ⊥ AB, BD ⊥ AB và AB = AC = BD. Xác định thiết diện của tứ diện ABCD khi cắt bởi mặt phẳng (α) đi qua điểm A và vuông góc với CD. Tính diện tích thiết diện khi AC = AB = BD = a.
Giải
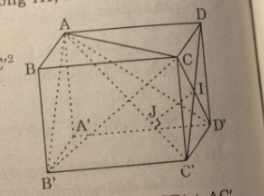
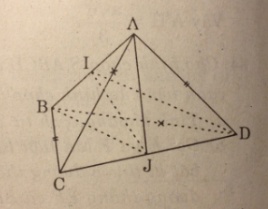
Gọi I là trung điểm của BC thì AI ⊥ BC. Do BD ⊥ mp(ABC) nên AI ⊥ CD (định lí ba đường vuông góc).
Trong mp(CDB), kẻ IJ vuông góc với CD (J ϵ CD) thì mp(AIJ) chính là mặt phẳng (α) và thiết diện phải tìm là tam giác AIJ
Tam giác AIJ là tam giác vuông tại I.
Vậy \({S_{AIJ}} = {1 \over 2}AI.IJ\)
Ta có:
\(\eqalign{ & AI = {1 \over 2}BC = {{a\sqrt 2 } \over 2} \cr & {{IJ} \over {DB}} = {{CI} \over {CD}} \Rightarrow IJ = {{CI} \over {CD}}.DB = {{{{a\sqrt 2 } \over 2}} \over {a\sqrt 3 }}.a = {{a\sqrt 6 } \over 6} \cr} \)
Vậy \({S_{AIJ}} = {1 \over 2}.{{a\sqrt 2 } \over 2}.{{a\sqrt 6 } \over 6} = {{{a^2}\sqrt 3 } \over {12}}\)
Chia sẻ trang này
Các bài học liên quan
Các chương học và chủ đề lớn
- Chương i. hàm số lượng giác và phương trình lượng giác
- Chương ii. tổ hợp và xác suất
- Chương iii. dãy số. cấp số cộng và cấp số nhân
- Chương iv. giới hạn
- Chương v. đạo hàm
- Ôn tập cuối năm đại số và giải tích
- Chương i. phép dời hình và đồng dạng trong mặt phẳng
- Chương ii: đường thẳng và mặt phẳng trong không gian. quan hệ song song
- Chương iii: vectơ trong không gian. quan hệ vuông góc
- Ôn tập cuối năm hình học
