Giải câu 9 trang 13 SGK Hình học 11 Nâng cao
Chia sẻ trang này
Cho góc nhọn
- Bài học cùng chủ đề:
- Câu 10 trang 13 SGK Hình học 11 Nâng cao
- Câu 11 trang 14 SGK Hình học 11 Nâng cao
- Ngữ pháp tiếng anh hay nhất
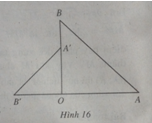
Bài 9. Cho góc nhọn xOy và một điểm A nằm trong góc đó. Hãy xác định điểm B trên Ox và điểm C trên Oy sao cho tam giác ABC có chu vi nhỏ nhất
Giải
Xét tam giác bất kì ABC có B và C lần lượt nằm trên hai tia Ox và Oy.
Gọi A’ và A” là các điểm đối xứng với điểm A lần lượt qua các đường thẳng Ox và Oy.
Ta có \(AB = A’B\) và \(AC = A”C\) ( do các \(△ABA’\) và \(△ACA”\) là các tam giác cân).
Gọi \(2p\) là chu vi của tam giác ABC thì: \(2p = AB + BC + CA = A’B + BC + CA” ≥ A’A”\)
Dấu “=” xảy ra khi bốn điểm \(A’, B, C, A”\) thẳng hàng.
Suy ra để chu vi tam giác ABC bé nhất thì phải lấy B và C lần lượt là giao điểm của đoạn thẳng A’A” với hai tia Ox và Oy (các giao điểm đó tồn tại vì góc xOy nhọn)
Chia sẻ trang này
Các bài học liên quan
Các chương học và chủ đề lớn
- Chương i. hàm số lượng giác và phương trình lượng giác
- Chương ii. tổ hợp và xác suất
- Chương iii. dãy số. cấp số cộng và cấp số nhân
- Chương iv. giới hạn
- Chương v. đạo hàm
- Ôn tập cuối năm đại số và giải tích
- Chương i. phép dời hình và đồng dạng trong mặt phẳng
- Chương ii: đường thẳng và mặt phẳng trong không gian. quan hệ song song
- Chương iii: vectơ trong không gian. quan hệ vuông góc
- Ôn tập cuối năm hình học
