Giải câu 13 trang 18 SGK Hình học 11 Nâng cao
Cho hai tam giác vuông cân OAB
- Bài học cùng chủ đề:
- Câu 14 trang 18 SGK Hình học 11 Nâng cao
- Câu 15 trang 18 SGK Hình học 11 Nâng cao
- Câu 16 trang 19 SGK Hình học 11 Nâng cao
- Ngữ pháp tiếng anh hay nhất
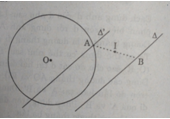
Bài 13. Cho hai tam giác vuông cân OAB và OA'B' có chung đỉnh O sao cho O nằm trên đoạn thẳng A'B' và nằm ngoài đoạn thẳng A'B (h.16). Gọi G và G' lần lượt là trọng tâm các tam giác OAA' và OBB'.Chứng minh GOG' là tam giác vuông cân.

Giải
Gọi Q là phép quay tâm O, góc quay \({\pi \over 2}\) (bằng góc lượng giác (OA ; OB)). Khi đó Q biến A thành B và biến A’ thành B’, tức là biến tam giác OAA’ và OBB’
Bởi vậy Q biến G (trọng tâm tam giác OAA’) thành G’ (trọng tâm tam giác OBB’).
Suy ra \(OG = OG’\) và \(\widehat {GOG'} = {\pi \over 2}\)
Vậy GOG’ là tam giác vuông cân tại đỉnh O

Chú ý: Phép quay Q biến trọng tâm G tam giác ABC thành trọng tâm G’ của tam giác A’B’C’ ảnh của △ABC qua Q được suy ra từ phép quay Q biến trung điểm I của đoạn thẳng
- Chương i. hàm số lượng giác và phương trình lượng giác
- Chương ii. tổ hợp và xác suất
- Chương iii. dãy số. cấp số cộng và cấp số nhân
- Chương iv. giới hạn
- Chương v. đạo hàm
- Ôn tập cuối năm đại số và giải tích
- Chương i. phép dời hình và đồng dạng trong mặt phẳng
- Chương ii: đường thẳng và mặt phẳng trong không gian. quan hệ song song
- Chương iii: vectơ trong không gian. quan hệ vuông góc
- Ôn tập cuối năm hình học