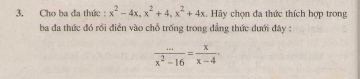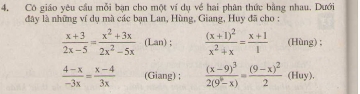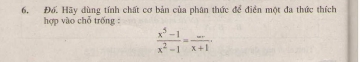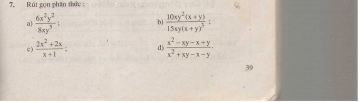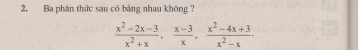
Giải bài 81 trang 33 sgk toán 8 tập 1
Chia sẻ trang này
Tìm x, biết:
- Bài học cùng chủ đề:
- Bài 82 trang 33 sgk toán 8 tập 1
- Bài 83 trang 33 sgk toán 8 tập 1
- Ngữ pháp tiếng anh hay nhất
Bài 81. Tìm \(x\), biết:
a) \({2 \over 3}x\left( {{x^2} - 4} \right) = 0\) ;
b) \({\left( {x + 2} \right)^2} - \left( {x - 2} \right)\left( {x + 2} \right) = 0\) ;
c) \(x + 2\sqrt 2 {x^2} + 2{x^3} = 0\) .
Giải
a) \({2 \over 3}x\left( {{x^2} - 4} \right) = 0\)
\({2 \over 3}x\left( {{x^2} - {2^2}} \right) = 0\)
\({2 \over 3}x\left( {x - 2} \right)\left( {x + 2} \right) = 0\)
Hoặc \(x = 0\)
Hoặc \(x – 2 = 0 \Rightarrow x = 2\)
Hoặc \(x + 2 = 0 \Rightarrow x = -2\)
Vậy \(x = 0,x = - 2,x = 2\)
b) \({\left( {x + 2} \right)^2} - \left( {x - 2} \right)\left( {x + 2} \right) = 0\)
\(\left( {x + 2} \right)\left[ {\left( {x + 2} \right) - \left( {x - 2} \right)} \right] = 0\)
\(\left( {x + 2} \right)\left( {x + 2 - x + 2} \right) = 0\)
\(\left( {x + 2} \right).4 = 0\)
\(x + 2 = 0\)
\(x = - 2\)
Vậy \(x=-2\)
c) \(x + 2\sqrt 2 {x^2} + 2{x^3} = 0\)
\(x\left( {1 + 2\sqrt 2 x + 2{x^2}} \right) = 0\)
\(x(1^2 + 2\sqrt 2 x .1+ {\left( {\sqrt 2 x} \right)^2}) = 0\)
\(x{\left( {1 + \sqrt 2 x} \right)^2} = 0\)
Hoặc \(x = 0\)
Hoặc \({\left( {1 + \sqrt 2 x} \right)^2} = 0 \Rightarrow 1 + \sqrt 2 x = 0\Rightarrow x = - {1 \over {\sqrt 2 }}\)
Vậy \(x = 0,x = - {1 \over {\sqrt 2 }}\)
Chia sẻ trang này
Các bài học liên quan
Các chương học và chủ đề lớn
