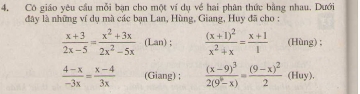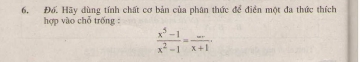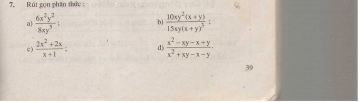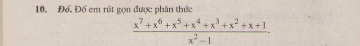Giải bài 83 trang 33 sgk toán 8 tập 1
Tìm n để phân thức chia hết cho 2n +1.
Bài 83. Tìm \(n \in\mathbb Z\) để \(2{n^2} - n + 2\) chia hết cho \(2n +1\).
Giải
Ta có: \({{2{n^2} - n + 2} \over {2n + 1}} = {{2{n^2} + n - 2n - 1 + 3} \over {2n + 1}}\)
=\({{n\left( {2n + 1} \right) - \left( {2n + 1} \right) + 3} \over {2n + 1}} = {{\left( {2n + 1} \right)\left( {n - 1} \right) + 3} \over {2n + 1}} = n - 1 + {3 \over {2n + 1}}\)
Để \(2{n^2} - n + 2\) chia hết cho \(2n + 1\) (với \(n \in\mathbb Z)\) thì \(2n + 1\) phải là ước của \(3\). Do đó:
\(2n + 1 = 1 = > 2n = 0 = > n = 0\)
\(2n + 1 = - 1 = > 2n = - 2 = > n = - 1\)
\(2n + 1 = 3 = > 2n = 2 = > n = 1\)
\(2n + 1 = - 3 = > 2n = - 4 = > n = - 2\)
Vậy \(n = 0; -1; -2; 1\)
Trên đây là bài học "Giải bài 83 trang 33 sgk toán 8 tập 1" mà dayhoctot.com muốn gửi tới các em. Để rèn luyện về kỹ năng làm bài thi và kiểm tra các em tham khảo tại chuyên mục "Đề thi học kì 1 lớp 8" nhé.
Nếu thấy hay, hãy chia sẻ tới bạn bè để cùng học và tham khảo nhé! Và đừng quên xem đầy đủ các bài Giải bài tập Toán Lớp 8 của dayhoctot.com.
Các bài học liên quan
Bài 4. Cô giáo yêu cầu mỗi bạn cho một ví dụ về hai phân thức đại số bằng nhau. Dưới đây là những ví dụ các bạn lan, hùng, hương, huy đã cho:
Bài 5. Điền đa thức thích hợp vào mỗi chỗ trống trong các đẳng thức sau:
Bài 6. Đố. Hãy dùng tính chất cơ bản của phân thức để điền một đa thức thích hợp vào chỗ trống:
Bài 7. Rút gọn phân thức:
Bài 8. Trong một tờ nháp của một bạn có ghi một số phép rút gọn phân thức như sau:
Bài 9. Áp dụng quy tắc đổi dấu rồi rút gọn phân thức:
Bài 10. Đố em rút gọn được phân thức:
Các chương học và chủ đề lớn
Học tốt các môn khác lớp 8