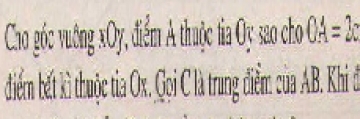Giải bài 65 trang 100 sgk toán 8 tập 1

Chia sẻ trang này

Tứ giác ABCD có hai đường chéo vuông góc với nhau. Gọi

Bài 65. Tứ giác \(ABCD\) có hai đường chéo vuông góc với nhau. Gọi \(E, F, G, H\) theo thứ tự là trung điểm của các cạnh \(AB, BC, CD, DA\). Tứ giác \(EFGH\) là hình gì ? Vì sao ?

Bài giải:

Ta có \(EB = EA, FB = FC\) (do \(E,F\) là trung điểm của \(AB,BC\))

\(EF\) là đường trung bình của \(∆ABC\)

Do đó \(EF // AC\) (1)

Do \(G,H\) là trung điểm của \(CD,DA) nên

\( HG\) là đường trung bình của \(∆ADC\)

Do đó \(HG // AC\) (2)

Từ (1) và (2) suy ra \(EF // HG\)

Chứng minh tương tự \(EH // FG\)

Do đó \(EFGH\) là hình bình hành.

Ta có: \(EF // AC\) và \(EH//BD\) mà \(AC\bot BD\) nên \(EF\bot EH\)

Hay \(\widehat{FEH} = 90^0\)

Hình bình hành \(EFGH\) có \(\widehat{E} = 90^0\) nên là hình chữ nhật (theo dấu hiệu nhận biết hình chữ nhật).

Trên đây là bài học "Giải bài 65 trang 100 sgk toán 8 tập 1" mà dayhoctot.com muốn gửi tới các em. Để rèn luyện về kỹ năng làm bài thi và kiểm tra các em tham khảo tại chuyên mục "Đề thi học kì 1 lớp 8" nhé.

Nếu thấy hay, hãy chia sẻ tới bạn bè để cùng học và tham khảo nhé! Và đừng quên xem đầy đủ các bài Giải bài tập Toán Lớp 8 của dayhoctot.com.