Giải bài 55 trang 96 sgk toán 8 tập 1

Chia sẻ trang này

Cho hình bình hành ABCD, O là giao điểm của hai đường chéo. Một đường thẳng đi qua O cắt các cạnh AB và

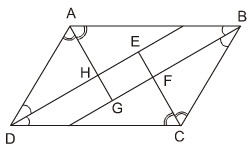
Bài 55. Cho hình bình hành \(ABCD\), \(O\) là giao điểm của hai đường chéo. Một đường thẳng đi qua \(O\) cắt các cạnh \(AB\) và \(CD\) theo thứ tự ở \(M\) và \(N\). Chứng minh rằng điểm \(M\) đối xứng với điểm \(N\) qua \(O\).

Bài giải:

Xét tam giác \(BOM\) và \(DON\) có

+) \(\widehat{B_{1}}\) = \(\widehat{D_{1}}\) (so le trong)

+) \(BO = DO\) (tính chất hình bình hành)

+) \(\widehat{O_{1}}\) = \(\widehat{O_{2}}\) (đối đỉnh)

Suy ra:\( ∆BOM = ∆DON (g.c.g)\)

Suy ra \(OM = ON\) (hai cạnh tương ứng).

Do đó \(O\) là trung điểm của \(MN\) nên \(M \) đối xứng với \(N\) qua \(O\).

Trên đây là bài học "Giải bài 55 trang 96 sgk toán 8 tập 1" mà dayhoctot.com muốn gửi tới các em. Để rèn luyện về kỹ năng làm bài thi và kiểm tra các em tham khảo tại chuyên mục "Đề thi học kì 1 lớp 8" nhé.

Nếu thấy hay, hãy chia sẻ tới bạn bè để cùng học và tham khảo nhé! Và đừng quên xem đầy đủ các bài Giải bài tập Toán Lớp 8 của dayhoctot.com.