Giải bài 51 trang 84 - Sách giáo khoa toán 8 tập 2
Bài 51 Chân đường cao AH của tam giác vuông ABC chia cạnh huyền BC thành hai đoạn có độ dài 25cm và 36cm. Tính chu vi và diện tích của tam giác vuông đó(h.53)
Bài 51 Chân đường cao AH của tam giác vuông ABC chia cạnh huyền BC thành hai đoạn có độ dài 25cm và 36cm. Tính chu vi và diện tích của tam giác vuông đó(h.53)
Hướng dẫn: Trước tiên tìm cách AH từ các tam giác vuông đồng dạng, sau đó tính các cạnh của tam giác ABC.

Giải:
∆AHB ∽ ∆CHA vì \(\widehat{AHB} = \widehat{AHC}\) = 900,
\(\widehat{BAH} = \widehat{ACH}\)
\(\frac{AH}{CH }= \frac{BH}{CH}\) => AH2 = CH.BH = 25.36
=> AH2 = 900 => AH = 300
Vậy \(S_{ABC}\) = \(\frac{1}{2}\) AH.BC = \(\frac{1}{2}\).30.(25 + 26) = 915 cm2
Trên đây là bài học "Giải bài 51 trang 84 - Sách giáo khoa toán 8 tập 2" mà dayhoctot.com muốn gửi tới các em. Để rèn luyện về kỹ năng làm bài thi và kiểm tra các em tham khảo tại chuyên mục "Đề thi học kì 1 lớp 8" nhé.
Nếu thấy hay, hãy chia sẻ tới bạn bè để cùng học và tham khảo nhé! Và đừng quên xem đầy đủ các bài Giải bài tập Toán Lớp 8 của dayhoctot.com.
Các bài học liên quan
Bài 55 Hình 58 dưới đây mô tả dụng cụ đo bề dày của một số loại sản phẩm. Dụng cụ này gồm thước AC được chia đến 1mm và gắn với một kim loại hình tam giác ABD, khoảng cách BC= 10cm.
Xác định tỉ số của hai đoạn thẳng AB và CD trong các trường hợp sau:
Cho tam giác ABC (AB < AC). Vẽ đường cao AH, đường phân giác AD, đường trung tuyến AM. Có nhận xét gì về vị trí của ba điểm H, D, M.
Cho tam giác cân ABC (AB = AC), vẽ các đường cao BH, CK (H.66
Hình thang ABCD (AB//CD) có AC và BD cắt nhau tại O, AD và BC cắt nhau tại K. Chứng minh rằng OK đi qua trung điểm của các cạnh AB và CD.
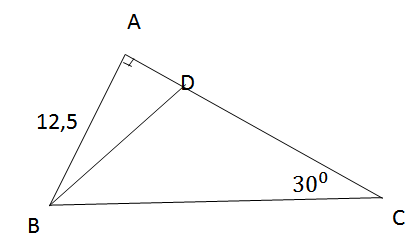
Cho tam giác vuông ABC, và đường phân giác BD (D thuộc cạnh AC).
Tứ giác ABCD có AB = 4cm, BC = 20 cm, CD = 25 cm, DA = 8cm, đường chéo BD = 10cm.
Các chương học và chủ đề lớn
Học tốt các môn khác lớp 8