Giải bài 65 trang 137 - Sách giáo khoa toán 7 tập 1
Bài 65. Các tam giác ABC cân tại A
Bài 65. Các tam giác ABC cân tại A(\(\widehat{A}\)<900). Vẽ BH ⊥ A (H thuộc AC), CK⊥ AB (K thuộc AB)
a) Chứng minh rằng AH=AK.
b) Gọi I là giao điểm của BH và CK. Chứng minh rằng tia AI là tia phân giác của góc A.
Giải:

a) Hai tam giác vuông ABH và ACK có:
AB = AC(gt)
Góc A chung.
nên ∆ABH = ∆ACK(Cạnh huyền- Góc nhọn)
suy ra AH = AK.
b) Hai tam giác vuông AIK và AIH có:
AK = AH(cmt)
AI cạnh chung
Nên ∆AIK = ∆AIH(cạnh huyền- cạnh góc vuông)
Suy ra \(\widehat{IAK}\)=\(\widehat{IAH}\)
Vậy AI là tia phân giác của góc A.
Trên đây là bài học "Giải bài 65 trang 137 - Sách giáo khoa toán 7 tập 1" mà dayhoctot.com muốn gửi tới các em. Để rèn luyện về kỹ năng làm bài thi và kiểm tra các em tham khảo tại chuyên mục "Đề thi học kì 1 lớp 7" nhé.
Nếu thấy hay, hãy chia sẻ tới bạn bè để cùng học và tham khảo nhé! Và đừng quên xem đầy đủ các bài Giải bài tập Toán Lớp 7 của dayhoctot.com.
Các bài học liên quan
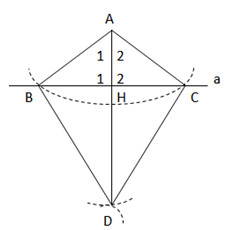
Vẽ các cung tròn tâm B và tâm C có bán kính sao cho chúng cắt nhau tại một điểm khác A, gọi điểm đó là D. Hãy giải thích vì sao AD vuông góc với đường thẳng a.
Cho tam giác ABC cân tại A. Trên tia đối của BC lấy điểm M, trên tia đối của tia CB lấy điểm N sao cho BM = CN.
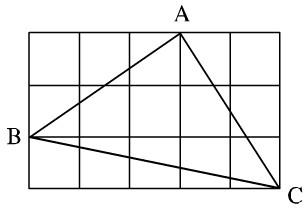
Tam giác ABC trên giấy kẻ ô vuông (h.151) là tam giác gì ? Vì sao ?
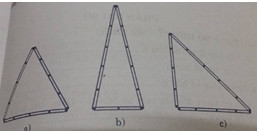
Đố vui: Dũng đố Cường dùng 12 que diêm bằng nhau để xếp thành:
a)Một tam giác đều ;
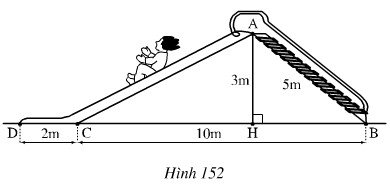
Đố:Bạn Mai nói rằng đường trượt tổng cộng ACD gấp hơn hai lần đường lên BA. Bạn Vân nói rằng điều đó không đúng. Ai đúng, ai sai?
Lập bảng số liệu thống kê cho một cuộc điều tra nhỏ về một dấu hiệu mà em quan tâm
Hàng ngày, bạn An thử ghi lại thời gian cần thiết để đi từ nhầ đến trường
Các chương học và chủ đề lớn
Học tốt các môn khác lớp 7