Giải bài 9 trang 71 sgk toán 8 tập 1
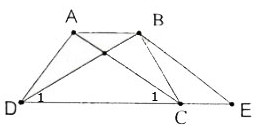
Tứ giác ABCD có AB= BC và tia phân giác cưa góc A. Chứng minh rằng ABCD là hình thang.
9. Tứ giác ABCD có AB= BC và tia phân giác của góc A. Chứng minh rằng ABCD là hình thang.
Bài giải:

Ta có AB = BC (gt)
Suy ra ∆ABC cân
Nên \(\widehat{A_{1}}=\widehat{C_{1}}\) (1)
Lại có \(\widehat{A_{1}}= \widehat{A_{2}}\) (2) (vì AC là tia phân giác của \(\widehat{A}\))
Từ (1) và (2) suy ra \(\widehat{C_{1}}=\widehat{A_{2}}\)
nên BC // AD (do \(\widehat{C_{1}},\widehat{A_{2}}\) ở vị trí so le trong)
Vậy ABCD là hình thang
Trên đây là bài học "Giải bài 9 trang 71 sgk toán 8 tập 1" mà dayhoctot.com muốn gửi tới các em. Để rèn luyện về kỹ năng làm bài thi và kiểm tra các em tham khảo tại chuyên mục "Đề thi học kì 1 lớp 8" nhé.
Nếu thấy hay, hãy chia sẻ tới bạn bè để cùng học và tham khảo nhé! Và đừng quên xem đầy đủ các bài Giải bài tập Toán Lớp 8 của dayhoctot.com.
Các bài học liên quan
Cho hình thang cân ABCD (AB // CD), E là giao điểm của hai đường chéo. Chứng minh rằng EA = EB, EC = ED.
Đố. Trong các tứ giác ABCD và EFGH trên giấy kẻ ô vuông (h.31), tứ giác nào là hình thang cân? Vì sao?
Cho tam giác ABC cân tại A. Trên các cạnh bên AB, AC lấy theo thứ tự các điểm D và E sao cho AD = AE.
Cho tam giác ABC cân tại A, các đường phân giác BD, CE (D ∈ AC, E ∈ AB). Chứng minh rằng BEDC là hình thang cân có đáy nhỏ bằng cạnh bên.
Hình thang ABCD (AB // CD) có
Chứng minh định lí "Hình thang có hai đường chéo bằng nhau là hình thang cân" qua bài toán sau: Cho hình thang ABCD
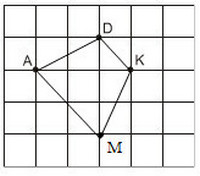
Đố. Cho ba điểm A, D, K trên giấy kẻ ô vuông (h.32). Hãy tìm điểm thứ tư M là giao điểm của các dòng kẻ sao cho nó cùng với
Các chương học và chủ đề lớn
Học tốt các môn khác lớp 8