Bài 3 trang 134 SGK Toán 9 tập 2
Cho tam giác ABC vuông ở C có đường trung tuyến BN vuông góc với đường trung tuyến CM, cạnh BC = a. Tính độ dài đường trung tuyến BN.
Bài 3. Cho tam giác \(ABC\) vuông ở \(C\) có đường trung tuyến \(BN\) vuông góc với đường trung tuyến \(CM\), cạnh \(BC = a\). Tính độ dài đường trung tuyến \(BN\).
Hướng dẫn trả lời:

Gọi \(G\) là trọng tâm của tam giác \(ABC\), ta có: \(BG = {2 \over 3}BN\)
Áp dụng hệ thức lượng trong tam giác vuông \(CNB\), ta có:
\(\eqalign{
& B{C^2} = BN.BG = BN.{2 \over 3}BN = {2 \over 3}B{N^2} \cr
& \Rightarrow B{N^2} = {3 \over 2}B{C^2} = {{3{a^2}} \over 2} \cr
& \Rightarrow BN = \sqrt {{{3{{\rm{a}}^2}} \over 2}} = {{a\sqrt 3 } \over {\sqrt 2 }} = {{a\sqrt 6 } \over 2} \cr}\)
Vậy \(BN = {{a\sqrt 6 } \over 2}\)
Trên đây là bài học "Bài 3 trang 134 SGK Toán 9 tập 2" mà dayhoctot.com muốn gửi tới các em. Để rèn luyện về kỹ năng làm bài thi và kiểm tra các em tham khảo tại chuyên mục "Đề thi học kì 1 lớp 9" nhé.
Nếu thấy hay, hãy chia sẻ tới bạn bè để cùng học và tham khảo nhé! Và đừng quên xem đầy đủ các bài Giải bài tập Toán Lớp 9 của dayhoctot.com.
Các bài học liên quan
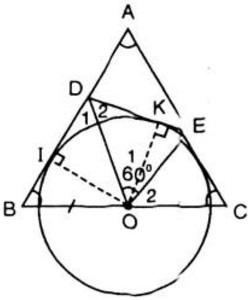
Cho tam giác đều ABC, O là trung điểm của BC. Trên các cạnh AB, AC lần lượt lấy các điểm di động D và E sao cho góc DOE = 60o.
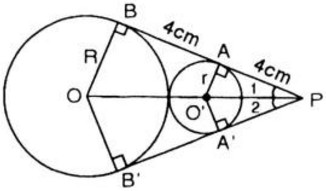
Cho hai đường tròn (O; R) và (O'; r) tiếp xúc ngoài (R > r). Hai tiếp tuyến chung AB và A'B' của hai đường tròn (o),(O') cắt nhau tại P(A và A' thuộc đường tròn (O'), B và B' thuộc đường tròn (O)). Biết PA = AB = 4 cm. Tính diện tích hình tròn (O').
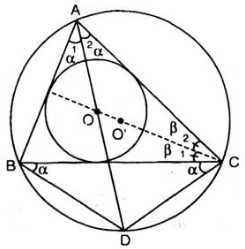
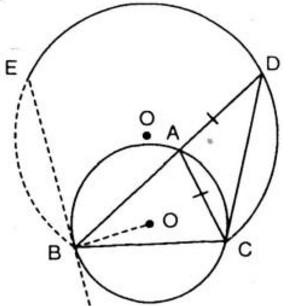
Cho tam giác ABC nội tiếp đường tròn (O') và ngoại tiếp đường tròn (O). Tia AO cắt đường tròn (O') tại D. Ta có:
Cho tam giác nhọn ABC nội tiếp đường tròn(O). Các cung nhỏ AB, BC, CA có số đo lần lượt là x + 75o, 2x + 25o, 3x - 22o. Một góc của tam giác ABC có số đo là:
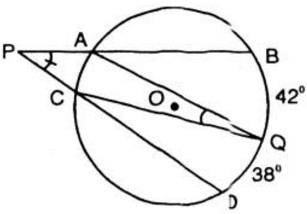
Từ một điểm P ở ngoài đường tròn (O), kẻ cát tuyến PAB và PCD tới đường tròn. Gọi Q là một điểm nằm trên cung nhỏ BD (không chứa A và C) sao cho sđ cung BQ = 42° và sđ cung QD = 38°. Tính tổng
Một hình vuông và một hình tròn có chu vi bằng nhau. Hỏi hình nào có diện tích lớn hơn?
Cho đường tròn (O), cung BC có số đo bằng 120o, điểm A di chuyển trên cung lớn BC. Trên tia đối tia AB lấy điểm D sao cho AD = AC. Hỏi điểm D di chuyển trên đường nào?
Các chương học và chủ đề lớn
Học tốt các môn khác lớp 9