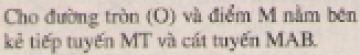
Giải bài 26 trang 76 sgk Toán lớp 9 tập 2
Chia sẻ trang này
Cho AB, BC, CA là ba dây của đường tròn (O).
- Bài học cùng chủ đề:
- Lý thuyết góc nội tiếp
- Ngữ pháp tiếng anh hay nhất
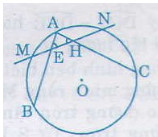
Bài 26. Cho \(AB, BC, CA \) là ba dây của đường tròn \((O)\). Từ điểm chính giữa \(M\) của \(\overparen{AB}\) vẽ dây \(MN\) song song với dây \(BC\). Gọi giao điểm của \(MN\) và \(AC\) là \(S\). Chứng minh \(SM = SC\) và \(SN = SA\)
Hướng dẫn giải:
Ta có:
\(\overparen{MA}\)= \(\overparen{MB}\) (theo gt).
\(\overparen{NC}\)= \(\overparen{MB}\) ( vì \(MN // BC\))
Suy ra \(\overparen{MA}\) = \(\overparen{NC}\), do đó \(\widehat {ACM} = \widehat {CMN}\)
Vậy \(∆SMC\) là tam giác cân, suy ra \(SM = SC\)
Chứng minh tương tự ta cũng có \(∆SAN\) cân , \(SN = SA\).
loigiaihay..com
Chia sẻ trang này
Các bài học liên quan
Các chương học và chủ đề lớn
