Giải bài 22 trang 76 sgk Toán lớp 9 tập 2
Chia sẻ trang này
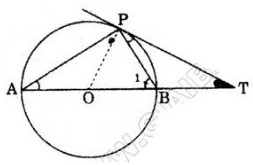
Bài 22. Trên đường tròn (O) đường kính AB
- Bài học cùng chủ đề:
- Bài 23 trang 76 sgk Toán lớp 9 tập 2
- Bài 24 trang 76 sgk Toán lớp 9 tập 2
- Bài 25 trang 76 sgk Toán lớp 9 tập 2
- Ngữ pháp tiếng anh hay nhất
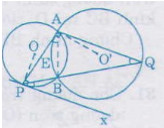
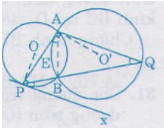
Bài 22. Trên đường tròn \((O)\) đường kính \(AB\), lấy điểm \(M\) (khác \(A\) và \(B\)). Vẽ đường qua \(A\) cắt \((O)\) tại \(A\). Đường thẳng \(BM\) cắt tiếp tuyến đó tại \(C\). Chứng minh rằng ta luôn có: \(M{A^2} = MB.MC\)
Hướng dẫn giải:
Ta có: \(∆MAB\) đồng dạng \(∆MCA\) (\(\widehat{A_{2}}\) = \(\widehat{C}\); \(\widehat{B}\) = \(\widehat{A_{1}}\))
nên \(\frac{MA}{MB}\) = \(\frac{MC}{MA}\)
Suy ra \(M{A^2} = MB.MC\)
Chia sẻ trang này
Các bài học liên quan
Các chương học và chủ đề lớn
