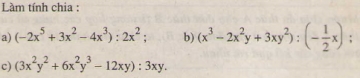Giải bài 54 trang 25 sgk toán 8 tập 1
Chia sẻ trang này
Phân tích các đa thức sau thành nhân tử:
- Bài học cùng chủ đề:
- Bài 55 trang 25 sgk toán 8 tập 1
- Bài 56 trang 25 sgk toán 8 tập 1
- Bài 57 trang 25 sgk toán 8 tập 1
- Ngữ pháp tiếng anh hay nhất
Bài 54. Phân tích các đa thức sau thành nhân tử:
a) \({x^3} + {\rm{ }}2{x^2}y{\rm{ }} + {\rm{ }}x{y^2}-{\rm{ }}9x\);
b) \(2x{\rm{ }}-{\rm{ }}2y{\rm{ }}-{\rm{ }}{x^2} + {\rm{ }}2xy{\rm{ }}-{\rm{ }}{y^2}\);
c) \({x^4}-{\rm{ }}2{x^2}\).
Bài giải:
a) \({x^3} + {\rm{ }}2{x^2}y{\rm{ }} + {\rm{ }}x{y^2}-{\rm{ }}9x{\rm{ }} = {\rm{ }}x({x^2}{\rm{ }} + 2xy{\rm{ }} + {\rm{ }}{y^2}-{\rm{ }}9)\)
\(= {\rm{ }}x[({x^2} + {\rm{ }}2xy{\rm{ }} + {\rm{ }}{y^2}){\rm{ }}-{\rm{ }}9]\)
\(= {\rm{ }}x[{\left( {x{\rm{ }} + {\rm{ }}y} \right)^2}-{\rm{ }}{3^2}]\)
\(= {\rm{ }}x\left( {x{\rm{ }} + {\rm{ }}y{\rm{ }}-{\rm{ }}3} \right)\left( {x{\rm{ }} + {\rm{ }}y{\rm{ }} + {\rm{ }}3} \right)\)
b) \(2x{\rm{ }}-{\rm{ }}2y{\rm{ }}-{\rm{ }}{x^2} + {\rm{ }}2xy{\rm{ }}-{\rm{ }}{y^2} = {\rm{ }}\left( {2x{\rm{ }}-{\rm{ }}2y} \right){\rm{ }}-{\rm{ }}({x^2}-{\rm{ }}2xy{\rm{ }} + {\rm{ }}{y^2})\)
\(= {\rm{ }}2\left( {x{\rm{ }}-{\rm{ }}y} \right){\rm{ }}-{\rm{ }}{\left( {x{\rm{ }}-{\rm{ }}y} \right)^2}\)
\( = {\rm{ }}\left( {x{\rm{ }}-{\rm{ }}y} \right)\left[ {2{\rm{ }}-{\rm{ }}\left( {x{\rm{ }}-{\rm{ }}y} \right)} \right]\)
\(= (x – y)(2 – x + y)\)
c) \({x^4}-{\rm{ }}2{x^2} = {\rm{ }}{x^2}\left( {{x^2} - 2} \right){\rm{ = }}{{\rm{x}}^2}\left( {{x^2} - {{\left( {\sqrt 2 } \right)}^2}} \right) \)
\(={x^2}\left( {x{\rm{ }} - {\rm{ }}\sqrt 2 } \right)\left( {x{\rm{ }} + {\rm{ }}\sqrt 2 } \right)\).
Chia sẻ trang này
Các bài học liên quan
Các chương học và chủ đề lớn
