Giải bài 34 trang 128 sgk toán lớp 8 tập 1
Bài 34. Cho một hình chữ nhật. Vẽ tứ giác có các đỉnh là trung điểm các cạnh của hình chữ nhật . Vì sao tứ giác này là một hình thoi?
Bài 34. Cho một hình chữ nhật. Vẽ tứ giác có các đỉnh là trung điểm các cạnh của hình chữ nhật . Vì sao tứ giác này là một hình thoi? So sánh diện tích hình thoi và diện tích hình chữ nhật, từ đó suy ra cách tính diện tích hình thoi.
Hướng dẫn giải:
Vẽ hình chữ nhật ABCD với các trung điểm các cạnh M, N, P, Q.
Vẽ tứ giác MNPQ

Ta có MN = PQ = \(\frac{1}{2}\)BD
NP = MQ = \(\frac{1}{2}\) AC
Mà AC = BD
Nên tứ giác MNPQ là hình thoi vì có bốn cạnh bằng nhau.
Dễ dàng chứng minh rằng : ∆AMN = ∆INM , ∆BPN = ∆NIP
∆PCQ = ∆IQP, ∆DMQ = IQM
Do đó
SMNPQ = \(\frac{1}{2}\) SABCD mà SABCD = AB. AD = MP. NQ
Vậy SMNPQ = \(\frac{1}{2}\) MP.NQ
Trên đây là bài học "Giải bài 34 trang 128 sgk toán lớp 8 tập 1" mà dayhoctot.com muốn gửi tới các em. Để rèn luyện về kỹ năng làm bài thi và kiểm tra các em tham khảo tại chuyên mục "Đề thi học kì 1 lớp 8" nhé.
Nếu thấy hay, hãy chia sẻ tới bạn bè để cùng học và tham khảo nhé! Và đừng quên xem đầy đủ các bài Giải bài tập Toán Lớp 8 của dayhoctot.com.
Các bài học liên quan
Bài 38. Một con đường cắt một đám đất hình chữ nhật với các dữ liệu được cho trên hình 153
Bài 39. Thực hiện các phép vẽ và đo cần thiết để tính diện tích một đám đất có dạng như hình 154
Bài 40.Tính diện tích thực của hồ nước có sơ đồ là phần gạch sọc trên hình 155
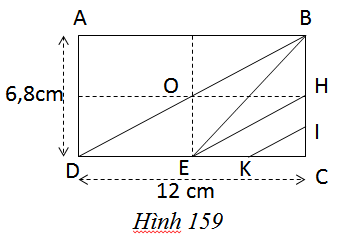
Cho hình chữ nhật ABCD. Gọi H, I, E, K lần lượt là các trung điểm của BC, HD, DC, EC (h.159)
Tính: a)Diện tích tam giác DBE ;
b)Diện tích tứ giác EHIK.
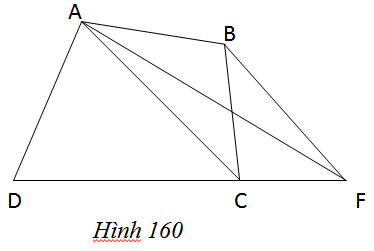
Trên hình 160 (AC//BF), hãy tìm tam giác có diện tích bằng diện tích của tứ giác ABCD.
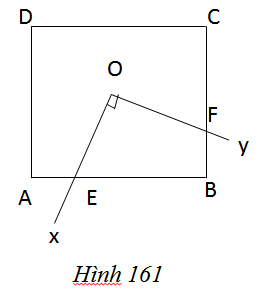
Cho hình vuông ABCD có tâm đối xứng O, cạnh a. Một góc vuông xOy có tia Ox cắt cạnh AB tại E, tia Oy cắt cạnh BC tại F (h.161)
Tính diện tích tứ giác OEBF.
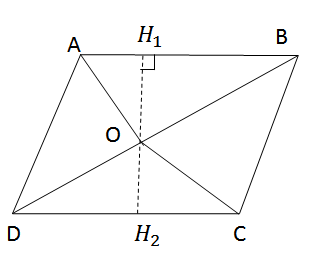
Gọi O là điểm nằm trong hình bình hành ABCD. Chứng minh rằng tổng diện tích của hai tam giác ABO và CDO bằng tổng diện tích của hai tam giác BCO và DAO.
Các chương học và chủ đề lớn
Học tốt các môn khác lớp 8