Giải bài 13 trang 131 sgk toán 8 tập 2
Một xí nghiệp dự định sản xuất 1500 sản phẩm trong 30 ngày. Nhưng nhờ tổ chức lao động hợp lí nên thực tế đã sản xuất mỗi ngày vượt 15 sản phẩm.
Một xí nghiệp dự định sản xuất 1500 sản phẩm trong 30 ngày. Nhưng nhờ tổ chức lao động hợp lí nên thực tế đã sản xuất mỗi ngày vượt 15 sản phẩm.
Do đó xí nghiệp đã sản xuất không những vượt mức dự định 225 sản phẩm mà còn hoàn thành trước thời hạn. Hỏi thực tế xí nghiệp đã rút ngắn được bao nhiêu ngày?
Hướng dẫn làm bài
Gọi số ngày rút bớt là x \((0 \le x < 30)\)
Số sản phẩm trong một ngày theo dự định ban đầu là \({{1500} \over {30}}\) (sản phẩm).
Tổng số sản phẩm sản xuất được sau khi đã tăng năng suất :
1500 + 255 = 1755 (sản phẩm)
Số sản phẩm sản xuất trong một ngày sau khi đã tăng năng suất
\({{1755} \over {30 - x}}\) (sản phẩm)
Theo đề bài ta có phương trình :
\({{1755} \over {30 - x}} - {{1500} \over {30}} = 15 \Leftrightarrow {{1755} \over {30 - x}} - 50 = 15 \Leftrightarrow {{1755} \over {30 - x}} = 65\)
⇔1755 = 65( 30 – x )
⇔1755 = 1950 – 65 x
⇔65x = 1950 – 1755
⇔65 x = 195
⇔x = 3 (thỏa mãn)
Vậy xí nghiệp đã rút ngắn được 3 ngày.
Trên đây là bài học "Giải bài 13 trang 131 sgk toán 8 tập 2" mà dayhoctot.com muốn gửi tới các em. Để rèn luyện về kỹ năng làm bài thi và kiểm tra các em tham khảo tại chuyên mục "Đề thi học kì 1 lớp 8" nhé.
Nếu thấy hay, hãy chia sẻ tới bạn bè để cùng học và tham khảo nhé! Và đừng quên xem đầy đủ các bài Giải bài tập Toán Lớp 8 của dayhoctot.com.
Các bài học liên quan
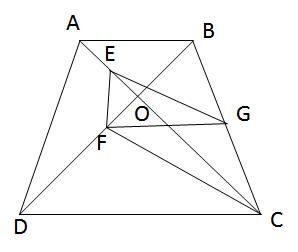
Cho hình thang ABCD (AB // CD) có hai đường chéo cắt nhau ở O và tam giác ABO là tam giác đều. Gọi E, F, G theo thứ tự là trung điểm của các đoạn thẳng OA, OD và BC. Chứng minh rằng tam giác EFG là tam giác đều.
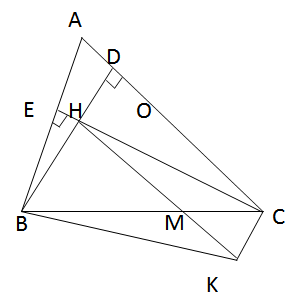
Tam giác ABC có các đường cao BD, CE cắt nhau tại H. Đường vuông góc với AB tại B và đường vuông góc với AC tại C cắt nhau ở K. Tam giác ABC phải có điều kiện gì thì tứ giác BHCK là:
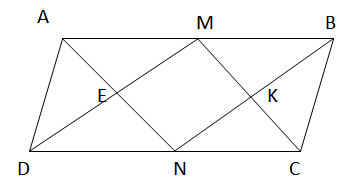
Cho hình bình hành ABCD. Các điểm M, N theo thứ tự là trung điểm của AB, CD. Gọi E là giao điểm của AN và DM, K là giao điểm của BN và CM. Hình bình hành ABCD phải có điều kiện gì để tứ giác MENK là:
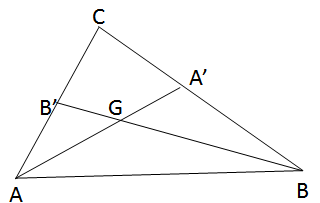
Trong tam giác ABC các đường trung tuyến AA’ và BB’ cắt nhau ở G. Tính diện tích tam giác ABC biết rằng diện tích tam giác ABG bằng S.
Cho tam giác ABC và đường trung tuyến BM. Trên đoạn thẳng BM lấy điểm D sao cho . Tia AD cắt BC ở K. Tìm tỉ số diện tích của tam giác ABK và tam giác ABC.
Cho tam giác ABC (AB < AC). Tia phân giác của góc A cắt BC ở K. Qua trung điểm M của BC kẻ một tia song song với KA cắt đường thẳng AB ở D, cắt AC ở E. Chứng minh BD = CE.
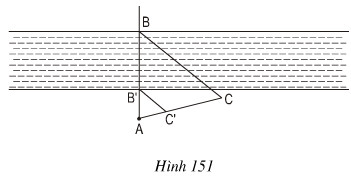
Trên hình 151 cho thấy ta có thể xác định chiều rộng BB’ của khúc song bằng cách xét hai tam giác đồng dạng ABC và AB’C’. Hãy tính BB’ nếu AC = 100 m, AC’ = 32 m, AB’ = 34m.
Các chương học và chủ đề lớn
Học tốt các môn khác lớp 8