Giải bài 39 trang 79 - Sách giáo khoa toán 8 tập 2
Bài 39 Cho hình thang ABCD(AB//CD). Gọi O là giao điểm của hai đường chéo AC và BD.
Bài 39 Cho hình thang ABCD(AB//CD). Gọi O là giao điểm của hai đường chéo AC và BD.
a) Chứng minh rằng OA.OD = OB.OC.
b) Đường thẳng qua O vuông góc với AB và CD theo thứ tự tại H và K.
Chứng minh rằng \(\frac{OH}{OK}\) = \(\frac{AB}{CD}\)
Giải:

a) Vì AB // CD => ∆AOB ∽ ∆COD
=> \(\frac{OA}{OC}\) = \(\frac{OB}{OD}\) => OA.OD = OC.OB
b) ∆AOH và ∆COK có:
\(\widehat{AHO}\) = \(\widehat{CKO}\) = 900
\(\widehat{HOA}\) = \(\widehat{KOC}\)
=> ∆AOH ∽ ∆COK
=> \(\frac{OH}{OK}\) = \(\frac{OA}{OC}\) (1)
mà \(\frac{OA}{OC}\) = \(\frac{AB}{CD}\) (2)
Từ 1 và 2 => \(\frac{OH}{OK}\) = \(\frac{AB}{CD}\)
Trên đây là bài học "Giải bài 39 trang 79 - Sách giáo khoa toán 8 tập 2" mà dayhoctot.com muốn gửi tới các em. Để rèn luyện về kỹ năng làm bài thi và kiểm tra các em tham khảo tại chuyên mục "Đề thi học kì 1 lớp 8" nhé.
Nếu thấy hay, hãy chia sẻ tới bạn bè để cùng học và tham khảo nhé! Và đừng quên xem đầy đủ các bài Giải bài tập Toán Lớp 8 của dayhoctot.com.
Các bài học liên quan
Bài 43 Cho hình bình hành ABCD(h46) có độ dài các cạnh AB = 12cm, BC = 7cm. Trên cạnh AB lấy một điểm E sao cho AE = 8cm. Đường thẳng DE cắt CB kéo dài tại F,
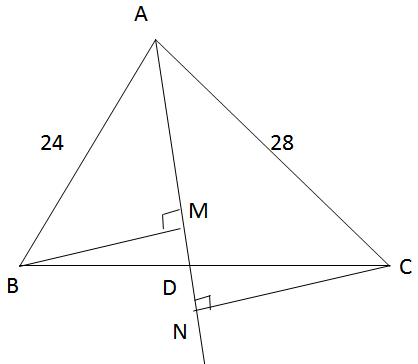
Cho tam giác ABC có các cạnh AB = 24 cm, AC = 28 cm. Tia phân giác của góc A cắt cạnh BC tại D. Gọi M, N theo thứ tự là hình chiếu của B và C trên đường thẳng AD.
Bài 45 Hai tam giác ABC và DEF có...
Bài 46 Trên hình 50, hãy chỉ ra các tam giác đồng dạng. Viết các tam giác này theo thứ tự đỉnh tương ứng và giải thích vì sao chúng đồng dạng?
Bài 47 Tam giác ABC có độ dài các cạnh là 3cm, 4cm, 5cm. Tam giác A\'B\'C\' đồng dạng với tam giác ABC và có diện tích là 54
Bài 48. Bóng của một cột điện trên mặt đất có độ dài là 4.5m. Cùng thời điểm đó, một thanh sắt cao 2,1m cắm vuông góc với mặt đất có bóng dài 0,6m.
Bài 49 Ở hình 51, tam giác ABC vuông tại A có đường cao AH
Các chương học và chủ đề lớn
Học tốt các môn khác lớp 8