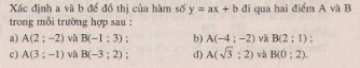
Giải bài 21 trang 19 sgk Toán 9 tập 2
Chia sẻ trang này
Giải các hệ phương trình sau bằng phương pháp cộng đại số.
- Bài học cùng chủ đề:
- Bài 22 trang 19 sgk Toán 9 tập 2
- Bài 23 trang 19 sgk Toán 9 tập 2
- Bài 24 trang 19 sgk toán 9 tập 2
- Ngữ pháp tiếng anh hay nhất
21. Giải các hệ phương trình sau bằng phương pháp cộng đại số.
a) \(\left\{\begin{matrix} x\sqrt{2} - 3y = 1 & & \\ 2x + y\sqrt{2}=-2 & & \end{matrix}\right.\);
b) \(\left\{\begin{matrix} 5x\sqrt{3}+ y = 2\sqrt{2}& & \\ x\sqrt{6} - y \sqrt{2} = 2& & \end{matrix}\right.\)
Bài giải:
a) \(\left\{\begin{matrix} x\sqrt{2} - 3y = 1 & & \\ 2x + y\sqrt{2}=-2 & & \end{matrix}\right.\) ⇔ \(\left\{\begin{matrix} -2x + 3\sqrt{2}.y = -\sqrt{2}& & \\ 2x + y\sqrt{2} = -2& & \end{matrix}\right.\)
⇔ \(\left\{\begin{matrix} 4\sqrt{2}.y = -\sqrt{2} - 2& & \\ 2x + y\sqrt{2} = -2& & \end{matrix}\right.\)⇔ \(\left\{\begin{matrix} x = -1 - \frac{\sqrt{2}}{2}y& & \\ y = \frac{-1- \sqrt{2}}{4}& & \end{matrix}\right.\)⇔ \(\left\{\begin{matrix} x = -\frac{3}{4} + \frac{\sqrt{2}}{8}& & \\ y = -\frac{1}{4} - \frac{\sqrt{2}}{4}& & \end{matrix}\right.\)
b) Nhân phương trình thứ nhất với \(\sqrt{2}\) rồi cộng từng vế hai phương trình ta được:
\(5x\sqrt{6} + x\sqrt{6} = 6 ⇔ x = \frac{1}{\sqrt{6}}\)
Từ đó hệ đã cho tương đương với \(\left\{\begin{matrix} x = \frac{1}{\sqrt{6}} & & \\ x\sqrt{6} - y\sqrt{2} = 2 & & \end{matrix}\right.\) ⇔ \(\left\{\begin{matrix} x = \frac{1}{\sqrt{6}} & & \\ y = -\frac{1}{\sqrt{2}} & & \end{matrix}\right.\)
Chia sẻ trang này
Các bài học liên quan
Các chương học và chủ đề lớn
