Giải bài 19 trang 75 sgk Toán lớp 9 tập 2

Chia sẻ trang này

Bài 19. Cho một đường tròn tâm O

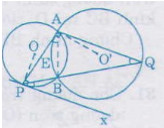
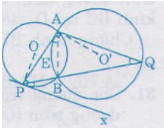
Bài 19. Cho một đường tròn tâm \(O\), đường kính \(AB\) và \(S\) là một điểm nằm ngoài đường tròn. \(SA\) và \(SB\) lần lượt cắt đường tròn tại \(M, N\). Gọi \(H\) là giao điểm của \(BM\) và \(AN\). Chứng minh rằng \(SH\) vuông góc với \(AB\).

Hướng dẫn giải:

\(BM \bot SA\) (\(\widehat{AMB}\) = \(90^{\circ}\) vì là góc nội tiếp chắn nửa đường tròn).

Tương tự, có: \(AN \bot SB\)

Như vậy \(BM\) và \(AN\) là hai đường cao của tam giác \(SAB\) và \(H\) là trực tâm.

Suy ra \(SH \bot AB\).

(Trong một tam giác ba đường cao đồng quy)

Trên đây là bài học "Giải bài 19 trang 75 sgk Toán lớp 9 tập 2" mà dayhoctot.com muốn gửi tới các em. Để rèn luyện về kỹ năng làm bài thi và kiểm tra các em tham khảo tại chuyên mục "Đề thi học kì 1 lớp 9" nhé.

Nếu thấy hay, hãy chia sẻ tới bạn bè để cùng học và tham khảo nhé! Và đừng quên xem đầy đủ các bài Giải bài tập Toán Lớp 9 của dayhoctot.com.