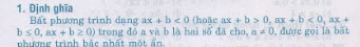Lý thuyết phương trình đưa được về dạng ax + b = 0
- Để giải các phương trình đưa được về ax + b = 0 ta thường biến đổi phương trình như sau:
- Để giải các phương trình đưa được về ax + b = 0 ta thường biến đổi phương trình như sau:
+ Quy đồng mẫu hai vế và khử mẫu.
+ thức hiện phép tính để bỏ dấu ngoặc và chuyển vế các hạng tử để đưa phương trình về dạng ax = c
+ TÌm x
Chú ý: Quá trình biến đổi phương trình về dạng ax = c có thể dẫn đến trường hợp đặc biệt là hệ số của ẩn bằng 0 nếu:
0x = c thì phương trình vô nghiệm S = Φ.
0x = 0 thì phương trình nghiệm đúng với mọi x hay vô số nghiệm: S = R.
Trên đây là bài học "Lý thuyết phương trình đưa được về dạng ax + b = 0" mà dayhoctot.com muốn gửi tới các em. Để rèn luyện về kỹ năng làm bài thi và kiểm tra các em tham khảo tại chuyên mục "Đề thi học kì 1 lớp 8" nhé.
Nếu thấy hay, hãy chia sẻ tới bạn bè để cùng học và tham khảo nhé! Và đừng quên xem đầy đủ các bài Giải bài tập Toán Lớp 8 của dayhoctot.com.
Các bài học liên quan
1. Liên hệ giữa thứ tự và phép nhân với số dương
1. Bất phương trình một ẩn
1. Nhắc lại về giá trị tuyệt đối
1.Tỉ số của hai đoạn thẳng. a) Định nghĩa:- Tỉ số của hai đoạn thẳng là tỉ số độ dài của chúng theo cùng một đơn vị đo.
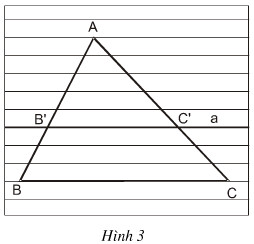
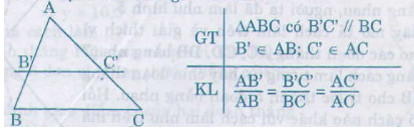
Nếu một đường thẳng cắt hai cạnh một tam giác và định ra trên hai cạnh ấy những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác.
Các chương học và chủ đề lớn
Học tốt các môn khác lớp 8