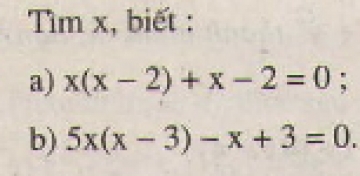
Giải bài 45 trang 20 sgk toán 8 tập 1
Chia sẻ trang này
Tìm x, biết:
- Bài học cùng chủ đề:
- Bài 46 trang 21 sgk toán 8 tập 1
- Ngữ pháp tiếng anh hay nhất
Bài 45. Tìm \(x\), biết:
a) \(2 – 25x^2= 0\); b) \(x^2- x + \frac{1}{4} = 0\)
Bài giải:
Ta có:
\(A.B = 0 \Rightarrow \left[ \matrix{
A = 0 \hfill \cr
B = 0 \hfill \cr} \right.\)
Trong đó \(A,B\) là các biểu thức.
a) \(2 – 25x^2= 0 \Rightarrow (\sqrt2)^2 – (5x)^2 = 0\)
\( \Rightarrow (\sqrt 2 – 5x)( \sqrt 2 + 5x) = 0\)
Đặt \(\sqrt 2 – 5x=A\)
\( \sqrt 2 + 5x=B\)
Do đó ta có: \(A.B = 0 \Rightarrow \left[ \matrix{
A = 0 \hfill \cr
B = 0 \hfill \cr} \right.\)
\( \Rightarrow \left[ \matrix{
\sqrt 2 + 5x = 0 \hfill \cr
\sqrt 2 - 5x = 0 \hfill \cr} \right. \Rightarrow \left[ \matrix{
x = - {{\sqrt 2 } \over 5} \hfill \cr
x = {{\sqrt 2 } \over 5} \hfill \cr} \right.\)
b) \(x^2- x + \frac{1}{4} = 0 \Rightarrow x^2– 2 . x . \frac{1}{2} + (\frac{1}{2})^2= 0\)
\(\Rightarrow (x - \frac{1}{2})^2= 0 \)
Đặt \(x - \frac{1}{2}=A\)
\(\Rightarrow A^2=0\Rightarrow A=0\)
\( \Rightarrow x - \frac{1}{2}= 0 \Rightarrow x = \frac{1}{2}\)
Chia sẻ trang này
Các bài học liên quan
Các chương học và chủ đề lớn
