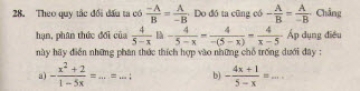Giải bài 20 trang 43 sgk toán 8 tập 1
Chia sẻ trang này
Cho hai phân thức: Không dùng cách phân tích các mẫu thức thành nhân tử, hãy chứng tỏ rằng có thể quy đồng mẫu thức hai phân thức này với mẫu thức chung
- Bài học cùng chủ đề:
- Lý thuyết quy đồng mẫu thức nhiều phân thức
- Ngữ pháp tiếng anh hay nhất
Cho hai phân thức:
\({1 \over {{x^2} + 3x - 10}}\) , \({x \over {{x^2} + 7x + 10}}\)
Không dùng cách phân tích các mẫu thức thành nhân tử, hãy chứng tỏ rằng có thể quy đồng mẫu thức hai phân thức này với mẫu thức chung là
\({x^3} + 5{x^2} - 4x - 20\)
Hướng dẫn làm bài:
Để chứng tỏ rằng có thể chọn đa thức \({x^3} + 5{x^2} - 4x - 20\) làm mẫu thức chung ta chỉ cần chứng tỏ rằng nó chia hết cho mẫu thức của mỗi phân thức đã cho.
Thật vậy, ta có:
\({x^3} + 5{x^2} - 4x - 20 = \left( {{x^2} + 3x - 10} \right)\left( {x + 2} \right)\)
\( = \left( {{x^2} + 7x + 10} \right)\left( {x - 2} \right)\)
Nên MTC = \({x^3} + 5{x^2} - 4x - 20\)
\({1 \over {{x^2} + 3x - 10}} = {{1\left( {x + 2} \right)} \over {\left( {{x^2} + 3x - 10} \right)\left( {x + 2} \right)}} = {{x + 2} \over {{x^3} + 5{x^2} - 4x - 20}}\)
\({x \over {{x^2} + 7x + 10}} = {{x\left( {x - 2} \right)} \over {\left( {{x^2} + 7x + 10} \right)\left( {x - 2} \right)}} = {{{x^2} - 2x} \over {{x^3} + 5{x^2} - 4x - 20}}\)
Chia sẻ trang này
Các bài học liên quan
Các chương học và chủ đề lớn
