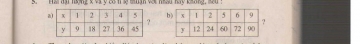Lý thuyết lũy thừa của một số hữu tỉ
Lũy thừa bậc n ( n là số tự nhiên lớn hơn 1) của một số hữu tỉ x là tích của n thừa số bằng x
1. Lũy thừa với số mũ tự nhiên
Lũy thừa bậc n ( n là số tự nhiên lớn hơn 1) của một số hữu tỉ x là tích của n thừa số bằng x
\({x^n} = \underbrace {x \ldots x}_{n:thừa số}\) ( x ∈ Q, n ∈ N, n> 1)
Nếu \(x = {a \over b}\) thì \({x^n} = {\left( {{a \over b}} \right)^n} = {{{a^n}} \over {{b^n}}}\)
Quy ước: a0 = 1 ( a ∈ N*)
x0 = 1 ( x ∈ Q, x # 0)
2. Tích của hai lũy thừa cùng cơ số
\({x^m}.{x^n} = {x^{m + n}}\) ( x ∈ Q; m, n ∈ N)
3. Thương của hai lũy thừa cùng cơ số khác 0
\({x^m}:{x^n} = {x^{m - n}}\) ( x ≠ 0, m ≥ n)
4. Lũy thừa của lũy thừa
\({\left( {{x^m}} \right)^n} = {x^{m.n}}\)
Trên đây là bài học "Lý thuyết lũy thừa của một số hữu tỉ" mà dayhoctot.com muốn gửi tới các em. Để rèn luyện về kỹ năng làm bài thi và kiểm tra các em tham khảo tại chuyên mục "Đề thi học kì 1 lớp 7" nhé.
Nếu thấy hay, hãy chia sẻ tới bạn bè để cùng học và tham khảo nhé! Và đừng quên xem đầy đủ các bài Giải bài tập Toán Lớp 7 của dayhoctot.com.
Các bài học liên quan
- Nếu một phân số tối giản với mẫu dương và mẫu không có ước nguyên tố khác 2 và 5 thì phân số đó viết được dưới dạng số thập phân hữu hạn - Nếu một phân số tối giản với mẫu dương và mẫu có ước nguyên tố khác 2 và 5 thì phân số đó viết dưới dạng số thập phân vô hạn tuần hoàn
Nếu chữ số đầu tiên bỏ đi nhỏ hơn 5 thì ta giữ nguyên bộ phận còn lại.
Số vô tỉ là số viết được dưới dạng số thập phân vô hạn không tuần hoàn.
Số hữu tỉ và số vô tỉ được gọi chung là số thực.
Bài 5. Hai địa lượng x và y tỉ lệ thuận với nhau hay không, nếu:
Các chương học và chủ đề lớn
Học tốt các môn khác lớp 7