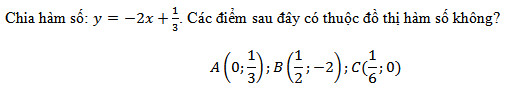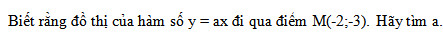Giải bài 62 trang 83 sgk toán lớp 7- tập 2
Chứng minh rằng một tam giác
62. Chứng minh rằng một tam giác có hai đường cao (xuất phát từ các đỉnh của hai góc nhọn) bằng nhau thì tam giác đó là tam giác cân. Từ đó suy ra một tam giác có ba đường cao bằng nhau thì tam giác đó là tam giác đều.
Hướng dẫn:

Xét hai tam giác vuông EBC và FCB có:
BC (cạnh huyền chung)
BE = CF
Vậy ∆EBC = ∆FCB (cạnh huyền cạnh góc vuông)
=> \(\widehat{FBC}= \widehat{ECB}\)
hay ∆ABC cân tại A
+ Nếu tam giác có ba đường cao bằng nhau, tương tự như chứng minh trên, ta chứng minh được đó là tam giác đều.
Trên đây là bài học "Giải bài 62 trang 83 sgk toán lớp 7- tập 2" mà dayhoctot.com muốn gửi tới các em. Để rèn luyện về kỹ năng làm bài thi và kiểm tra các em tham khảo tại chuyên mục "Đề thi học kì 1 lớp 7" nhé.
Nếu thấy hay, hãy chia sẻ tới bạn bè để cùng học và tham khảo nhé! Và đừng quên xem đầy đủ các bài Giải bài tập Toán Lớp 7 của dayhoctot.com.
Các bài học liên quan
Ba đơn vị kinh doanh đầu tư vốn tỉ lệ với 2:5 và 7. Hỏi mỗi đơn vị được chia bao nhiêu lãi nếu số tiền lãi là 560 triệu đồng và tiền lãi được chia tỉ lệ thuận với vốn đầu tư?
Chia hàm số: y = -2x+1/3. Các điểm sau đây có thuộc đồ thị hàm số không?
Biết rằng đồ thị của hàm số y = ax đi qua điểm M(-2;-3). Hãy tìm a.
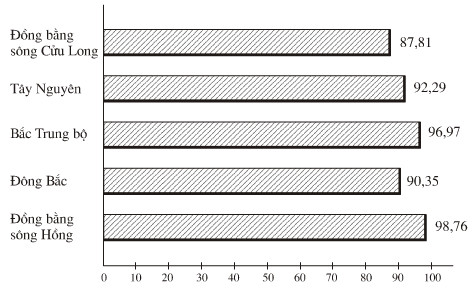
Biểu đồ dưới đây biểu diễn tỉ lệ (%) trẻ em từ 6 đến 10 tuổi đang học Tiểu học ở một số vùng của nước ta:
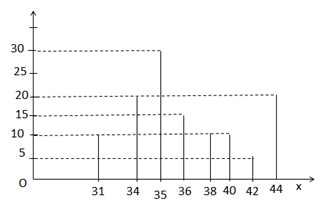
Để tìm hiểu về sản lượng vụ mùa của một xã, người ta chọn 120 thửa để gặt thử và ghi lại sản lượng của từng thửa (tính theo tạ/ha). Kết quả được tạm sắp xếp như sau:
Tính giá trị của biểu thức 2,7c^2 – 3,5c lần lượt tại c = 0,7; 2/3
Các chương học và chủ đề lớn
Học tốt các môn khác lớp 7