Giải bài 7 trang 69 sgk Toán 9 - tập 1
Chia sẻ trang này
Người ta đưa ra hai cách vẽ đoạn trung bình nhân x của hai đoạn thẳng a, b.
- Bài học cùng chủ đề:
- Bài 8 trang 70 sgk Toán 9 - tập 1
- Bài 9 trang 70 sgk Toán 9 - tập 1
- Lý thuyết một số hệ thức về cạnh và đường cao trong tam giác vuông
- Ngữ pháp tiếng anh hay nhất
Bài 7. Người ta đưa ra hai cách vẽ đoạn trung bình nhân x của hai đoạn thẳng a, b (tức là \({x^2} = ab\) ) như trong hai hình sau:
Dựa vào các hệ thức (1) và (2), hãy chứng minh các cách vẽ trên là đúng.
Gợi ý: Nếu một tam giác có đường trung tuyến ứng với một cạnh bằng nửa cạnh đó thì tam giác ấy là tam giác vuông.
Hướng dẫn giải:
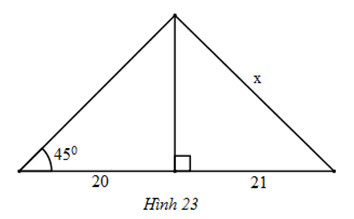
Cách 1: Đặt tên các đoạn thẳng như hình bên.
Xét tam giác ABC ta có:
\(OA = OB = OC = {{BC} \over 2}\left( { = R} \right)\)
Suy ra ∆ABC vuông tại A.
Áp dụng hệ thức \({h^2} = b'c' \Rightarrow {x^2} = ab\)
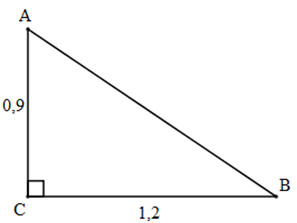
Cách 2: Vẽ và đặt tên như hình bên dưới
Xét tam giác ABC ta có:
\(OA = OB = OC = {{BC} \over 2}\left( { = R} \right)\)
Suy ra ∆ABC vuông tại A.
Áp dụng hệ thức \(A{B^2} = BC.BH \Rightarrow {x^2} = ab\).
Chia sẻ trang này
Các bài học liên quan
Các chương học và chủ đề lớn
