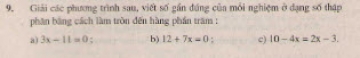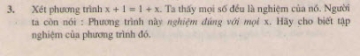
Giải bài 46 trang 133 sgk toán 8 tập 1
Chia sẻ trang này
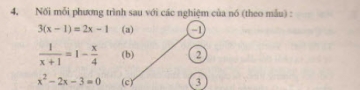
Cho tam giác ABC. Gọi M, N là các trung điểm tương ứng của AC, BC. Chứng minh rằng diện tích của hình thang ABNM bằng 3/4 diện tích của tam giác ABC.
- Bài học cùng chủ đề:
- Bài 47 trang 133 sgk toán 8 tập 1
- Ngữ pháp tiếng anh hay nhất
Cho tam giác ABC. Gọi M, N là các trung điểm tương ứng của AC, BC. Chứng minh rằng diện tích của hình thang ABNM bằng diện tích của tam giác ABC.
Hướng dẫn làm bài:
Vẽ hai trung tuyến AN, BM của ∆ABC. Ta có:
\({S_{ABN}} = {1 \over 2}{S_{ABC}}\)
(có cùng đường cao từ đỉnh A, đáy \(BN = {1 \over 2}BC)\)
\({S_{AMN}} = {S_{MNC}}\) (có cùn đường cao từ đỉnh N, đáy AM = MC).
Suy ra \({S_{AMN}} = {S_{MNC}} = {1 \over 2}{S_{ANC}} = {1 \over 4}{S_{ABC}}\)
Vậy \({S_{ABN}} + {S_{AMN}} = {1 \over 2}{S_{ABC}} + {1 \over 4}{S_{ABC}} = {3 \over 4}{S_{ABC}}\)
Tức là \({S_{ABMN}} = {3 \over 4}{S_{ABC}}\)
Chia sẻ trang này
Các bài học liên quan
Các chương học và chủ đề lớn
