Giải bài 31 trang 116 sgk Toán 9 - tập 1
Tam giác ABC ngoại tiếp đường tròn (O).
Trên hình 82, tam giác ABC ngoại tiếp đường tròn (O).

a) Chứng minh rằng:
\(2AD=AB+AC-BC.\)
b) Tìm các hệ thức tương tự hệ thức ở câu a).
Giải:
a) Theo tính chất của hai tiếp tuyến cắt nhau ta có:
\(AD=AF; BD=BE; CF=CE.\)
Xét vế phải:
\(AB+AC-BC\)
\(=(AD+DB)+(AF+FC)-(BE+EC)\)
\(=(AD+BE)+(AF+CE)-(BE+EC)\)
\(= AD+AF=2AD.\)
b) Các hệ thức tương tự là:
\(2BD=BA+BC-AC;\)
\(2CF=CA+CB-AB.\)
Nhận xét. Từ bài toán trên ta có các kết quả sau:
\(AD=AF=p-a;\)
\(BD=BE=p-b;\)
\(CE=CF=p-c\)
trong đó \(AB=c; BC=a; CA=b\) và p là nửa chu vi của tam giác ABC.
Trên đây là bài học "Giải bài 31 trang 116 sgk Toán 9 - tập 1" mà dayhoctot.com muốn gửi tới các em. Để rèn luyện về kỹ năng làm bài thi và kiểm tra các em tham khảo tại chuyên mục "Đề thi học kì 1 lớp 9" nhé.
Nếu thấy hay, hãy chia sẻ tới bạn bè để cùng học và tham khảo nhé! Và đừng quên xem đầy đủ các bài Giải bài tập Toán Lớp 9 của dayhoctot.com.
Các bài học liên quan
Điền vào các ô trống trong bảng, biết rằng hai đường tròn (O;R) và (O';r) có OO'=d, R>r.
Cho đường tròn tâm O bán kính OA và đường tròn đường kính OA.
Cho hai đường tròn đồng tâm O. Dây AB của đường tròn lớn cắt đường tròn nhỏ ở C và D. Chứng minh rằng AC=BD.
Điền các từ thích hợp vào chỗ trống (...)
Cho hai đường tròn (O) và (O') tiếp xúc ngoài tại A. Kẻ tiếp tuyến chung ngoài BC.
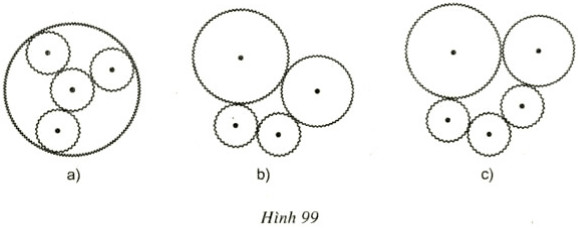
Trên các hình 99a, 99b, 99c, các bánh xe tròn có răng cưa được khớp với nhau. Trên hình nào hệ thống bánh răng chuyển động được? Trên hình nào hệ thống bánh răng không chuyển động được?
Cho đường tròn (O) có đường kính BC, dây AD vuông góc với BC tại H.Gọi E, F theo thứ tự là chân các đường vuông góc kẻ từ H đến AB, AC.
Các chương học và chủ đề lớn
Học tốt các môn khác lớp 9