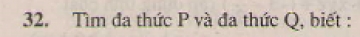Giải bài 25 trang 38 sgk toán 7 - tập 2

Chia sẻ trang này

Bài trước

Bài sau

Tìm bậc của mỗi đa thức sau:

Bài 25. Tìm bậc của mỗi đa thức sau:

a) 3x² – \(\frac{1}{2}\) x + 1 + 2x – x²;

b) 3x² + 7x³ – 3x³ + 6x³ – 3x².

Hướng dẫn giải:

a) \(3{x^2} - {1 \over 2}x + 1 + 2x - {x^2} \)

\(= \left( {3{x^2} - {x^2}} \right) + \left( { - {1 \over 2}x + 2x} \right) + 1 \)

\(= 2{x^2} + {3 \over 2}x + 1\)

Hạng tử \(2{x^2}\) có bậc 2

Hạng tử \({3 \over 2}x\) có bậc 1

1 có bậc 0

Vậy đa thức đã cho có bậc 2

\(\eqalign{
& 3{x^2} + 7{x^3} - 3{x^3} + 6{x^3} - 3{x^2} \cr
& = \left( {3{x^2} - 3{x^2}} \right) + \left( {7{x^3} + 6{x^3} - 3{x^3}} \right) \cr
& = 10{x^3} \cr} \)

Vậy đa thức đã cho có bậc 3

Trên đây là bài học "Giải bài 25 trang 38 sgk toán 7 - tập 2" mà dayhoctot.com muốn gửi tới các em. Để rèn luyện về kỹ năng làm bài thi và kiểm tra các em tham khảo tại chuyên mục "Đề thi học kì 1 lớp 7" nhé.

Nếu thấy hay, hãy chia sẻ tới bạn bè để cùng học và tham khảo nhé! Và đừng quên xem đầy đủ các bài Giải bài tập Toán Lớp 7 của dayhoctot.com.