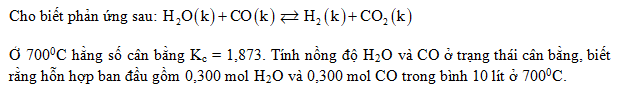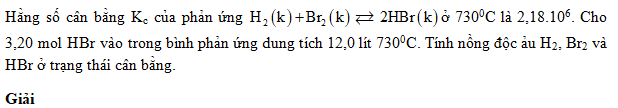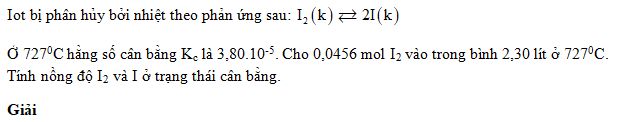Giải bài 3 trang 212 SGK Hóa học 10 Nâng cao

Chia sẻ trang này

Viết các biểu thức hằng số cân bằng Kc cho các phản ứng sau:

Viết các biểu thức hằng số cân bằng K_c cho các phản ứng sau:

\(\eqalign{
& a)\,\,CaC{O_3}\left( r \right)\,\, \mathbin{\lower.3ex\hbox{$\buildrel\textstyle\rightarrow\over
{\smash{\leftarrow}\vphantom{_{\vbox to.5ex{\vss}}}}$}} CaO\left( r \right) + C{O_2}\left( k \right) \cr
& b)\,\,C{u_2}O\left( r \right) + {1 \over 2}{O_2}\left( k \right)\,\, \mathbin{\lower.3ex\hbox{$\buildrel\textstyle\rightarrow\over
{\smash{\leftarrow}\vphantom{_{\vbox to.5ex{\vss}}}}$}} \,\,2CuO\left( r \right) \cr
& c)\,\,2S{O_2}\left( k \right) + {O_2}\left( k \right)\,\, \mathbin{\lower.3ex\hbox{$\buildrel\textstyle\rightarrow\over
{\smash{\leftarrow}\vphantom{_{\vbox to.5ex{\vss}}}}$}} 2S{O_3}\left( k \right)\,;\cr&S{O_2}\left( k \right) + {1 \over 2}{O_2}\left( k \right)\,\, \mathbin{\lower.3ex\hbox{$\buildrel\textstyle\rightarrow\over
{\smash{\leftarrow}\vphantom{_{\vbox to.5ex{\vss}}}}$}} \,\,S{O_3}\left( k \right)\,;\cr&2S{O_3}\left( k \right)\,\, \mathbin{\lower.3ex\hbox{$\buildrel\textstyle\rightarrow\over
{\smash{\leftarrow}\vphantom{_{\vbox to.5ex{\vss}}}}$}} \,\,2S{O_2}\left( k \right) + {O_2}\left( k \right) \cr} \)

Hãy cho biết mối liên hệ giữa ba hằng số cân bằng ứng với ba trường hợp trong câu c) ở cùng nhiệt độ.

Giải

Hằng số cân bằng của các phản ứng:

a) K_c = [CO₂].

b) ${K_c} = {1 \over {{{\left[ {{O_2}} \right]}^{{1 \over 2}}}}}$

c) ${K_{{C_1}}} = {{{{\left[ {S{O_3}} \right]}^2}} \over {{{\left[ {S{O_2}} \right]}^2}\left[ {{O_2}} \right]}};$

${K_{{C_2}}} = {{\left[ {S{O_3}} \right]} \over {\left[ {S{O_2}} \right]{{\left[ {{O_2}} \right]}^{{1 \over 2}}}}};$

${K_{{C_3}}} = {{{{\left[ {S{O_2}} \right]}^2}\left[ {{O_2}} \right]} \over {{{\left[ {S{O_3}} \right]}^2}}}$

Mối liên hệ giữa 3 hằng số ${K_{{C_1}}},{K_{{C_2}}},{K_{{C_3}}}$

${K_{{C_3}}} = {1 \over {{K_{{C_1}}}}};$

${K_{{C_2}}} = \sqrt {{K_{{C_1}}}} \,;$

${K_{{C_3}}} = {\left( {{1 \over {{K_{{C_2}}}}}} \right)^2} = {1 \over {K_{{C_2}}^2}}$

Trên đây là bài học "Giải bài 3 trang 212 SGK Hóa học 10 Nâng cao" mà dayhoctot.com muốn gửi tới các em. Để rèn luyện về kỹ năng làm bài thi và kiểm tra các em tham khảo tại chuyên mục "Đề thi học kì 1 lớp 10" nhé.

Nếu thấy hay, hãy chia sẻ tới bạn bè để cùng học và tham khảo nhé! Và đừng quên xem đầy đủ các bài Giải bài tập Hóa Học Lớp 10 của dayhoctot.com.