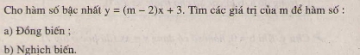
Giải bài 76 trang 41 SGK Toán 9 tập 1
Chia sẻ trang này
Cho biểu thức: a) Rút gọn Q b) Xác định giá trị của Q khi a = 3b
Cho biểu thức
\(Q = {a \over {\sqrt {{a^2} - {b^2}} }} - \left( {1 + {a \over {\sqrt {{a^2} - {b^2}} }}} \right):{b \over {a - \sqrt {{a^2} - {b^2}} }}\) với a > b > 0
a) Rút gọn Q
b) Xác định giá trị của Q khi a = 3b
Hướng dẫn làm bài:
a)
\(\eqalign{
& Q = {a \over {\sqrt {{a^2} - {b^2}} }} - \left( {1 + {a \over {\sqrt {{a^2} - {b^2}} }}} \right):{b \over {a - \sqrt {{a^2} - {b^2}} }} \cr
& = {a \over {\sqrt {{a^2} - {b^2}} }} - {{{a^2} - \left( {{a^2} - {b^2}} \right)} \over {b\sqrt {{a^2} - {b^2}} }} \cr
& = {a \over {\sqrt {{a^2} - {b^2}} }} - {{{a^2} - {a^2} + {b^2}} \over {b\sqrt {{a^2} - {b^2}} }} \cr
& = {{a - b} \over {\sqrt {{a^2} - {b^2}} }} = {{\sqrt {a - b} \sqrt {a - b} } \over {\sqrt {a + b} \sqrt {a - b} }} \cr
& = {{\sqrt {a - b} } \over {\sqrt {a + b} }} \cr}\)
b) Khi a = 3b. Giá trị của Q là
\({{\sqrt {3b - b} } \over {\sqrt {3b + b} }} = {{\sqrt {2b} } \over {4b}} = {{\sqrt {2b} } \over {\sqrt {2b} \sqrt 2 }} = {1 \over {\sqrt 2 }} = {{\sqrt 2 } \over 2}\)
Chia sẻ trang này
Các bài học liên quan
Các chương học và chủ đề lớn
