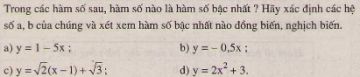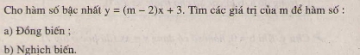
Giải bài 75 trang 40 SGK Toán 9 tập 1
Chia sẻ trang này
Chứng minh các đẳng thức sau:
- Bài học cùng chủ đề:
- Bài 76 trang 41 SGK Toán 9 tập 1
- Ngữ pháp tiếng anh hay nhất
Chứng minh các đẳng thức sau:
a) \(\left( {{{2\sqrt 3 - \sqrt 6 } \over {\sqrt 8 - 2}} - {{\sqrt {216} } \over 3}} \right).{1 \over {\sqrt 6 }} = - 1,5\)
b) \(\left( {{{\sqrt {14} - \sqrt 7 } \over {1 - \sqrt 2 }} + {{\sqrt {15} - \sqrt 5 } \over {1 - \sqrt 3 }}} \right):{1 \over {\sqrt 7 - \sqrt 5 }} = - 2\)
c) \({{a\sqrt b + b\sqrt a } \over {\sqrt {ab} }}:{1 \over {\sqrt a - \sqrt b }} = a - b\) với a, b dương và a ≠ b
d) \(\left( {1 + {{a + \sqrt a } \over {\sqrt a + 1}}} \right)\left( {1 - {{a - \sqrt a } \over {\sqrt a - 1}}} \right) = 1 - a\) với a ≥ 0 và a ≠ 1
Hướng dẫn làm bài:
a)
\(\eqalign{
& \left( {{{2\sqrt 3 - \sqrt 6 } \over {\sqrt 8 - 2}} - {{\sqrt {216} } \over 3}} \right).{1 \over {\sqrt 6 }} \cr
& = \left[ {{{\sqrt 6 \left( {\sqrt 2 - 1} \right)} \over {2\left( {\sqrt 2 - 1} \right)}} - {{6\sqrt 6 } \over 3}} \right].{1 \over {\sqrt 6 }} \cr
& = \left( {{{\sqrt 6 } \over 2} - 2\sqrt 6 } \right).{1 \over {\sqrt 6 }} \cr
& = \left( {{{ - 3} \over 2}\sqrt 6 } \right).{1 \over {\sqrt 6 }} \cr
& = - {3 \over 2} = - 1,5 \cr} \)
b)
\(\eqalign{
& \left( {{{\sqrt {14} - \sqrt 7 } \over {1 - \sqrt 2 }} + {{\sqrt {15} - \sqrt 5 } \over {1 - \sqrt 3 }}} \right):{1 \over {\sqrt 7 - \sqrt 5 }} \cr
& = \left[ {{{\sqrt 7 \left( {\sqrt 2 - 1} \right)} \over {1 - \sqrt 2 }} + {{\sqrt {5\left( {\sqrt 3 - 1} \right)} } \over {1 - \sqrt 3 }}} \right]:{1 \over {\sqrt 7 - \sqrt 5 }} \cr
& = \left( { - \sqrt 7 - \sqrt 5 } \right)\left( {\sqrt 7 - \sqrt 5 } \right) \cr
& = - \left( {\sqrt 7 + \sqrt 5 } \right)\left( {\sqrt 7 - \sqrt 5 } \right) \cr
& = - \left( {7 - 5} \right) = - 2 \cr} \)
c)
\(\eqalign{
& {{a\sqrt b + b\sqrt a } \over {\sqrt {ab} }}:{1 \over {\sqrt a - \sqrt b }} \cr
& = {{\sqrt {ab} \left( {\sqrt a + \sqrt b } \right)} \over {\sqrt {ab} }}.\left( {\sqrt a - \sqrt b } \right) \cr
& = a - b \cr} \)
d)
\(\eqalign{
& \left( {1 + {{a + \sqrt a } \over {\sqrt a + 1}}} \right)\left( {1 - {{a - \sqrt a } \over {\sqrt a - 1}}} \right) \cr
& = \left[ {1 + {{\sqrt a \left( {\sqrt a + 1} \right)} \over {\sqrt a + 1}}} \right]\left[ {1 - {{\sqrt a \left( {\sqrt a - 1} \right)} \over {\sqrt a - 1}}} \right] \cr
& = \left( {1 + \sqrt a } \right)\left( {1 - \sqrt a } \right) = 1 - a \cr} \)
Chia sẻ trang này
Các bài học liên quan
Các chương học và chủ đề lớn
