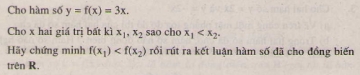
Giải bài 1 trang 44 sgk Toán 9 tập 1
Chia sẻ trang này
Cho hàm số y = f(x)
- Bài học cùng chủ đề:
- Bài 2 trang 45 sgk Toán 9 tập 1
- Bài 3 trang 45 sgk Toán 9 tập 1
- Bài 4 trang 45 sgk Toán 9 tập 1
- Ngữ pháp tiếng anh hay nhất
Bài 1.
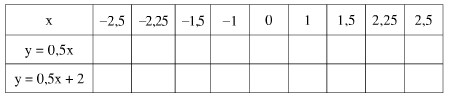
a) Cho hàm số \(y = f(x) = \frac{2}{3} x\).
Tính: \(f(-2); f(-1); f(0); f(\frac{1}{2}); f(1); f(2); f(3)\).
b) Cho hàm số \(y = g(x) = \frac{2}{3} x + 3\).
Tính: \(g(-2); g(-1); g(0); g(\frac{1}{2}); g(1); g(2); g(3)\).
c) Có nhận xét gì về giá trị của hai hàm số đã cho ở trên khi biến \(x\) lấy cùng một giá trị ?
Giải:
a) Thay các giá trị vào hàm số \(y = f(x) = \frac{2}{3} x\). Ta có
\(f(-2) = \frac{2}{3}.(-2)=\frac{-4}{3}\)
\(f(-1) = \frac{2}{3}.(-1)=\frac{-2}{3}\)
\(f(0) = \frac{2}{3}.(0)=0\)
\(f(\frac{1}{2}) = \frac{2}{3}.\left ( \frac{1}{2} \right )=\frac{1}{3}\)
\(f(1) = \frac{2}{3}.(1)=\frac{2}{3}\)
\(f(2) = \frac{2}{3}.(2)=\frac{4}{3}\)
\(f(3) = \frac{2}{3}.(3)=2\)
b) Thay các giá trị vào hàm số \(y = g(x) = \frac{2}{3} x + 3\). Ta có
\(g(-2) = \frac{2}{3}.(-2)+3=\frac{5}{3}\)
\(g(-1) = \frac{2}{3}.(-1)+3=\frac{7}{3}\)
\(g(0) = \frac{2}{3}.(0)+3=0\)
\(g\left ( \frac{1}{2} \right ) = \frac{2}{3}.\left ( \frac{1}{2} \right )+3=\frac{10}{3}\)
\(g(1) = \frac{2}{3}.(1)+3=\frac{11}{3}\)
\(g(2) = \frac{2}{3}.(2)+3=\frac{13}{3}\)
\(g(3) = \frac{2}{3}.(3)+3=5\)
c)
Khi \(x\) lấy cùng một giá trị thì giá trị của \(g(x)\) lớn hơn giá trị của \(f(x)\) là \(3\) đơn vị.
dayhoctot.com
Chia sẻ trang này
Các bài học liên quan
Các chương học và chủ đề lớn
