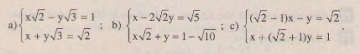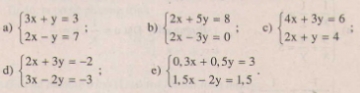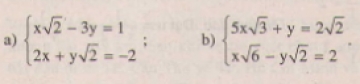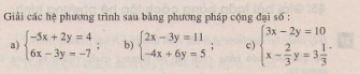
Giải bài 12 trang 15 sgk Toán 9 tập 2
Chia sẻ trang này
Giải các hệ phương trình sau bằng phương pháp thế:
- Bài học cùng chủ đề:
- Bài 13 trang 15 sgk Toán 9 tập 2
- Bài 14 trang 15 sgk Toán 9 tập 2
- Bài 15 trang 15 sgk Toán 9 tập 2
- Ngữ pháp tiếng anh hay nhất
12.Giải các hệ phương trình sau bằng phương pháp thế:
a) \(\left\{\begin{matrix} x - y =3 & & \\ 3x-4y=2 & & \end{matrix}\right.\);
b) \(\left\{\begin{matrix} 7x - 3y =5 & & \\ 4x+y=2 & & \end{matrix}\right.\);
c) \(\left\{\begin{matrix} x +3y =-2 & & \\ 5x-4y=11 & & \end{matrix}\right.\)
Bài giải:
a) Từ phương trình \(x - y = 3 \Rightarrow x = 3 + y\).
Thay \(x = 3 + y\) vào phương trình \(3x - 4y = 2\) ta được:
\(3(3 + y) - 4y = 2 ⇔ 9 + 3y - 4y = 2\)
\(⇔ -y = -7 ⇔ y = 7\)
Thay \(y = 7\) vào \(x = 3 + y\) ta được \(x = 3 + 7 = 10\).
Vậy hệ phương trình có nghiệm \((10; 7)\).
b) Từ phương trình \(4x + y = 2 \Rightarrow y = 2 - 4x\).
Thay \(y = 2 - 4x\) vào phương trình \( 7x - 3y = 5\) ta được:
\(7x - 3(2 - 4x) = 5 ⇔ 7x - 6 + 12x = 5\)
\(⇔ 19x = 11 ⇔ x = \frac{11}{19}\)
Thay \(x = \frac{11}{19}\) vào \(y = 2 - 4x\) ta được \(y = 2 - 4 . \frac{11}{19} = 2 - \frac{44}{19}= -\frac{6}{19}\)
Hệ phương trình có nghiệm (\(\frac{11}{19}\); -\(\frac{6}{19}\))
c) Từ phương trình \(x + 3y = -2 \Rightarrow x = -2 - 3y\).
Thay \(x=-2-3y\) vào phương trình \(5x - 4y = 11\) ta được:
\(5(-2 - 3y) - 4y = 11⇔ -10 - 15y - 4y = 11\)
\(⇔ -19y = 21 ⇔ y = -\frac{21}{19}\)
Thay \(y=-\frac{21}{19}\) vào \(x=-2-3y\) ta được \(x = -2 -3(-\frac{21}{19}) = -2 + \frac{63}{19} = \frac{25}{19}\)
Vậy hệ phương trình có nghiệm (\(\frac{25}{19}\); -\(\frac{21}{19}\)).
Chia sẻ trang này
Các bài học liên quan
Các chương học và chủ đề lớn
