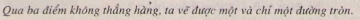Lý thuyết đồ thị của hàm số y = ax + b (a ≠ 0)
Chia sẻ trang này
Đồ thị của hàm số y = ax + b
A. Tóm tắt kiến thức:
1. Đồ thị hàm số y = ax + b (a ≠ 0).
Đồ thị của hàm số y = ax + b (a ≠ 0) là một đường thẳng:
- Cắt trục tung tại điểm có tung độ bằng b;
- Song song với đường thẳng y = ax nếu b ≠ 0 và trùng với đường thẳng y = ax nếu b = 0.
Đồ thị này cũng được gọi là đường thẳng y = ax + b và b được gọi là tung độ gốc của đường thẳng.
Lưu ý: Đồ thị y = ax + b cắt trục hoành tại điểm Q(-
; 0).
2. Cách vẽ đồ thị của hàm số y = ax + b (a ≠ 0).
- Chọn điểm P(0; b) (trên Oy).
- Chọn điểm Q (-; 0) (trên Ox).
- Kẻ đường thẳng PQ.
Lưu ý: Vì đồ thị y = ax + b (a ≠ 0) là một đường thẳng nên muốn vẽ nó chỉ cần xác định hai điểm phân biệt thuộc đồ thị.
Do đó trong trường hợp giá trị - khó xác định trên trục Ox thì ta có thể thay điểm Q bằng cách chọn một giá trị x1 của x sao cho điểm Q'(x1, y1 ) (trong đó y1 = ax1 + b) dễ xác định hơn trong mặt phẳng tọa độ.
Chia sẻ trang này
Các bài học liên quan
Các chương học và chủ đề lớn
