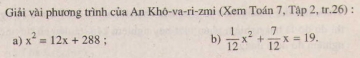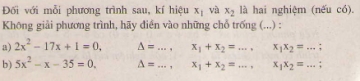Giải bài 15 trang 45 sgk Toán 9 tập 2
Chia sẻ trang này
Không giải phương trinh, hãy xác định các
- Bài học cùng chủ đề:
- Bài 16 trang 45 sgk Toán 9 tập 2
- Lý thuyết Công thức nghiệm của phương trình bậc hai
- Ngữ pháp tiếng anh hay nhất
Bài 15. Không giải phương trinh, hãy xác định các hệ số \(a, b, c\), tính biệt thức \(∆\) và xác định số nghiệm của mỗi phương trình sau:
a) \(7{x^2} - 2x + 3 = 0\)
b) \(5{x^2} + 2\sqrt {10} x + 2 = 0\);
c) \({1 \over 2}{x^2} + 7x + {2 \over 3} = 0\)
d) \(1,7{x^2} - 1,2x - 2,1=0\).
Bài giải:
a) \(7{x^2} - 2x + 3 = 0\)
\(a = 7,b = - 2,c = 3\)
\(\Delta = {( - 2)^2} - 4.7.3 = - 80\) vô nghiệm
b) \(5{x^2} + 2\sqrt {10} x + 2 = 0\)
\(a = 5,b = 2\sqrt {10} ,c = 2\)
\(\Delta = {(2\sqrt {10} )^2} - 4..5.2 = 0\) nghiệm kép
c) \({1 \over 2}{x^2} + 7x + {2 \over 3} = 0\)
\(a = {1 \over 2},b = 7,c = {2 \over 3}\)
\(\Delta = {7^2} - 4.{1 \over 2}.{2 \over 3} = {{143} \over 3}\). Phương trình có hai nghiệm phân biệt
d) \(1,7{x^2} - 1,2x - 2,1 = 0\)
\(a = 1,7,b = - 1,2,c = - 2,1\)
\(\Delta = {( - 1,2)^2} - 4..1,7.( - 2,1) = 15,72\).
Phương trình có hai nghiệm phân biệt.
Chia sẻ trang này
Các bài học liên quan
Các chương học và chủ đề lớn
