Giải bài 1 trang 99 sgk Toán 9 - tập 1
Chia sẻ trang này
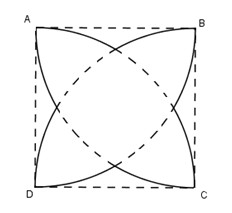
Cho hình chữ nhật ABCD có AB=12cm, BC=5cm. Chứng minh rằng bốn điểm A, B, C, D thuộc cùng một đường tròn.
- Bài học cùng chủ đề:
- Bài 2 trang 100 sgk Toán 9 - tập 1
- Bài 3 trang 100 sgk Toán 9 - tập 1
- Bài 4 trang 100 sgk Toán 9 - tập 1
- Ngữ pháp tiếng anh hay nhất
Cho hình chữ nhật ABCD có AB=12cm, BC=5cm. Chứng minh rằng bốn điểm A, B, C, D thuộc cùng một đường tròn. Tính bán kính của đường tròn đó.
Hướng dẫn giải:
Gọi O là giao điểm hai đường chéo của hình chữ nhật, ta có OA = OB = OC = OD = R.
Bốn điểm A, B, C, D, cách đều điểm O nên bốn điểm này cùng thuộc một đường tròn.
Xét tam giác ABC vuông tại B, có:
\(AC^{2}=AB^{2}+BC^{2}=12^{2}+5^{2}=169\Rightarrow AC=13.\)
Bán kính của đường tròn là \(R={13\over2}=6,5.\)
Nhận xét: Để chứng minh nhiều điểm cùng nằm trên một đường tròn, ta chứng minh các điểm này cùng cách đều một điểm.
Chia sẻ trang này
Các bài học liên quan
Các chương học và chủ đề lớn
