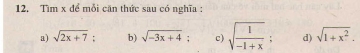Giải bài 4 trang 7 sgk Toán 9 - tập 1
Chia sẻ trang này
Bài 4. Tìm số x không âm, biết:a) √x = 15; b) 2√x =14; c)√x < √2; d) √2x < 4.
- Bài học cùng chủ đề:
- Bài 5 trang 7 sgk Toán 9 - tập 1
- Lý thuyết về căn bậc hai
- Ngữ pháp tiếng anh hay nhất
Bài 4. Tìm số x không âm, biết:
a) \(\sqrt{x}=15\); b) \(2\sqrt{x}=14\);
c) \(\sqrt{x}<\sqrt{2}\); d) \(\sqrt{2x}<4\).
Hướng dẫn giải:
Câu a:
Vận dụng điều lưu ý trong phần tóm tắt kiến thức bài học: "Nếu a ≥ 0 thì \(a = (\sqrt{a})^2\)":
Ta có:
\(\sqrt{x}=15\Leftrightarrow (\sqrt{x})^2=15^2\Leftrightarrow x=225\)
Câu b:
\(2\sqrt{x}=14\Leftrightarrow \sqrt{x}=\frac{14}{2}=7\Leftrightarrow (\sqrt{x})^2=7^2\Leftrightarrow x=49\)
Câu c:
Là một bất phương trình của hai số không âm, ta sẽ bình phương cả hai vế:
\(\sqrt{x}<\sqrt{2}\Leftrightarrow (\sqrt{x})^2<(\sqrt{2})^2\Leftrightarrow x<4\)
Câu d:
Là một bất phương trình của hai số không âm, ta bình phương cả hai vế:
\(\sqrt{2x}<4\Leftrightarrow (\sqrt{2x})^2<4^2\Leftrightarrow 2x<16\Leftrightarrow x<8\)
dayhoctot.com
Chia sẻ trang này
Các bài học liên quan
Các chương học và chủ đề lớn
