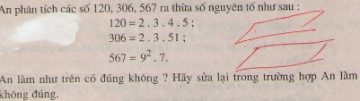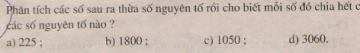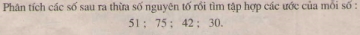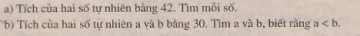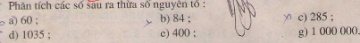
Giải bài 121 trang 47 sgk toán 6 tập 1

Chia sẻ trang này

Tìm số tự nhiên k để 3 . k là số nguyên tố.

Bài 121.

a) Tìm số tự nhiên \(k\) để \(3 . k\) là số nguyên tố.

b) Tìm số tự nhiên \(k\) để \(7 . k\) là số nguyên tố.

Bài giải:

a) Nếu \(k > 1\) thì \(3k\) có ít nhất ba ước là \(1, 3, 3k\); nghĩa là nếu \(k > 1\) thì \(3k\) là một hợp số. Do đó để \(3k\) là một số nguyên tố thì \(k = 1\).

b) Tương tự nếu \(k>1\) thì \(7k\) có ít nhất ba ước là \(1;7;7k\); nghĩa là nếu \(k>1\) thì \(7k\) là một hợp số. Do đó để \(7k\) là một số nguyên tố thì \(k=1\).

Trên đây là bài học "Giải bài 121 trang 47 sgk toán 6 tập 1" mà dayhoctot.com muốn gửi tới các em. Để rèn luyện về kỹ năng làm bài thi và kiểm tra các em tham khảo tại chuyên mục "Đề thi học kì 1 lớp 6" nhé.

Nếu thấy hay, hãy chia sẻ tới bạn bè để cùng học và tham khảo nhé! Và đừng quên xem đầy đủ các bài Giải bài tập Toán Lớp 6 của dayhoctot.com.