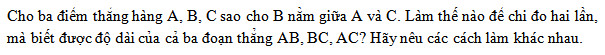Giải bài 64 trang 126 - Sách giáo khoa toán 6 tập 1
Bài 64 cho hai đoạn thẳng AB dài 6cm. Gọi C là trung điểm của AB lấy D và E là hai điểm thuộc đoạn thẳng AB sao cho AD=BE=2cm. Vì sao C là trung điểm của DE?
Bài 64 cho hai đoạn thẳng \(AB\) dài \(6cm\). Gọi \(C\) là trung điểm của \(AB\) lấy \(D\) và \(E\) là hai điểm thuộc đoạn thẳng \(AB\) sao cho \(AD=BE=2cm\). Vì sao \(C\) là trung điểm của \(DE\)?
Giải:

Vì \(C\) là trung điểm của \(AB\) nên \(C\) nằm giữa \(A\) và \(B\) và \(CA=CB= 6:2 = 3(cm)\).
Trên tia \(AB\) có: \(AD < AC (2<3)\) nên điểm \(D\) nằm giữa \(A\) và \(C\), do đó \(CD=AC-AD=3 – 2 = 1 (cm)\).
Trên tia \(BA\) có: \(BE<BC\) nên điểm \(E\) nằm giữa \(B\) và \(C\) và \(CE=BC-BE=3-2=1cm\).
Từ các dữ kiện trên suy ra điểm \(C\) nằm giữa \(D\) và \(E\).
Mặt khác có \(CD=CE(=1cm)\) nên \(C\) là trung điểm của \(D\) và \(E\).
Trên đây là bài học "Giải bài 64 trang 126 - Sách giáo khoa toán 6 tập 1" mà dayhoctot.com muốn gửi tới các em. Để rèn luyện về kỹ năng làm bài thi và kiểm tra các em tham khảo tại chuyên mục "Đề thi học kì 1 lớp 6" nhé.
Nếu thấy hay, hãy chia sẻ tới bạn bè để cùng học và tham khảo nhé! Và đừng quên xem đầy đủ các bài Giải bài tập Toán Lớp 6 của dayhoctot.com.
Các bài học liên quan
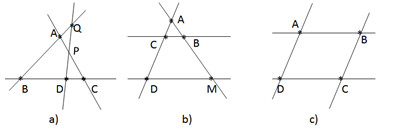
a) Đánh dấu hai điểm M, N. Vẽ đường thẳng a và đường thẳng xy cắt nhau tại M và đều không đi qua
Vẽ bốn đường thẳng phân biệt. Đặt tên cho các giao điểm (nếu có).
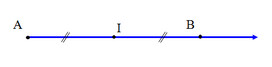
Cho ba điểm thẳng hàng A, B, C sao cho B nằm giữa A và C. Làm thế nào để chi đo hai lần, mà biết được độ dài của cả ba đoạn thẳng AB, BC, AC? Hãy nêu các cách làm khác nhau.
Cho đoạn thẳng AB dài 6 cm. Trên tia AB lấy điểm M sao cho AM = 3cm.
a)Điểm M có nằm giữa hai điểm A và B không?
b)So sánh AM và MB.
c)M có là trung điểm của AB không ?
Cho đoạn thẳng AB dài 7 cm. Vẽ trung điểm của đoạn thẳng AB.
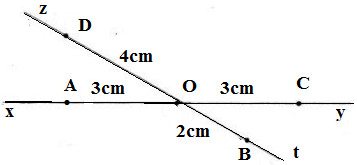
Vẽ hai đường thẳng xy và zt cắt nhau tại O. Lấy A thuộc tia Ox, B thuộc tia Ot, C thuộc tia Oy, D thuộc tia Oz sao cho OA = OC = 3cm, OB = 2 cm, OD = 2 OB.
Ta biểu diễn 1/4 của hình tròn bằng cách chia hình tròn bằng 4 phần bằng nhau rồi tô màu một phần như hình 1.
Các chương học và chủ đề lớn
Học tốt các môn khác lớp 6
![]()