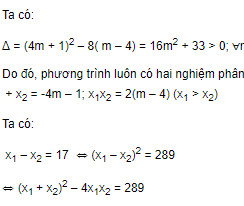Giải bài 14 trang 78 SGK Đại số 10 nâng cao

Bài trước
Bài sau  

Tìm nghiệm gần đúng của phương trình sau chính xác đến hàng phần trăm.

Tìm nghiệm gần đúng của phương trình sau chính xác đến hàng phần trăm.

a) \({x^2}– 5,6x + 6,41 = 0\);

b) \(\sqrt 2 {x^2} + 4\sqrt 3 x - 2\sqrt 2  = 0\)

Giải

a) \(Δ = 5,6^2 – 4.6,41 = 31,36 – 25,64 = 5,72\)

Phương trình có hai nghiệm phân biệt :

\({{x_1} = {\rm{ }}{{5,6 - \sqrt {5,72} } \over 2} \approx 1,60}\)

\({{x_2} = {{5,6 + \sqrt {5,72} } \over 2} \approx 4}\)

b) Viết phương trình dưới dạng tương đương:

\(\matrix{
2{x^2} + 4\sqrt 6 x-4 = 0 \hfill \cr
\Leftrightarrow {x^2} + 2\sqrt 6 x-2 = 0 \hfill \cr} \)

\(Δ’ = 6 + 2 = 8\), phương trình có hai nghiệm phân biệt :

\(\eqalign{
& {x_1} = - \sqrt 6 - \sqrt 8 \approx - 5,28 \cr
& {x_2} = - \sqrt 6 + \sqrt 8 \approx 0,28 \cr} \)

Bài trước
In bài này
Bài sau  
Các bài học liên quan
Các chương học và chủ đề lớn
Học tốt các môn khác lớp 10

Bài học nổi bật nhất

Đề thi lớp 10 mới cập nhật